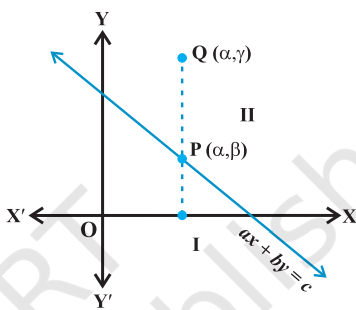
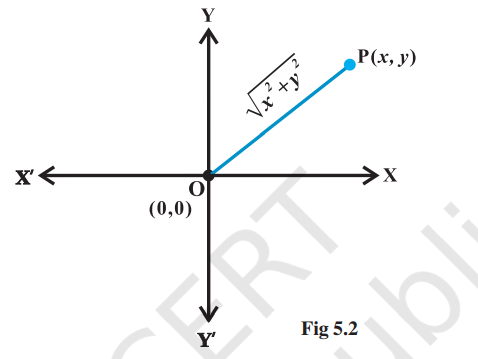
Coordinate Geometry, also known as Cartesian Geometry or Analytic Geometry, is a branch of mathematics that merges algebraic techniques with geometric intuition. It provides a powerful framework for representing geometric shapes and solving problems by introducing coordinates to the geometric objects. The Cartesian Coordinate System The cornerstone of coordinate geometry is the Cartesian Coordinate System, … Read more
A polynomial is a mathematical expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication operations. The general form of a polynomial is: \( P(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0 \) where \( a_n, a_{n-1}, \ldots, a_1, a_0 \) are coefficients, \( x \) is the variable, … Read more
Number systems are fundamental mathematical structures used to represent and manipulate numerical quantities. They provide a systematic way of expressing numbers, making mathematical operations and communication more efficient. Different number systems have evolved over time, each with its unique representation and set of rules. The three most commonly used number systems are the decimal (base-10), … Read more
Definition of Linear Inqualities Two real numbers or two algebraic expressions related by the symbol‘<’, ‘>’, ‘≤’ or ‘≥’ form an inequality 3 < 5; 7 > 5 are the examples of numerical inequalities x < 5; y > 2; x ≥ 3, y ≤ 4 are some examples of literal inequalities Keys point of … Read more
Let us denote √−1 by the symbol i . Then, we have i2 = −1 . This means that i is a solution of the equation x2 + 1 = 0 A number of the form a + ib, where a and b are real numbers, is defined to be a complex number For example, … Read more
In algebra or in other discipline of mathematics, there are certain results or statements that are formulated in terms of n, where n is a positive integer. To prove such statements the well-suited principle that is used–based on the specific technique, is known as the principle of mathematical induction In mathematics, we use a form … Read more
The word ‘trigonometry’ is derived from the Greek words ‘trigon’ and ‘metron’ and it means ‘measuring the sides of a triangle’. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others. Currently, trigonometry is used … Read more
From the definition of sine and cosine functions, we observe that they are defined for all real numbers. Further, we observe that for each real number x, – 1 ≤ sin x ≤ 1 and – 1 ≤ cos x ≤ 1 Thus, domain of y = sin x and y = cos x is … Read more
Let P (a, b) be a point on the unit circle with centre at the origin such that ∠AOP = x. If ∠AOQ = – x, then the coordinates of the point Q will be (a, –b) . Therefore cos (– x) = cos xand sin (– x) = – sin x Since for every … Read more
Consider a unit circle with centre at origin of the coordinate axes. Let P (a, b) be any point on the circle with angle AOP = x radian, i.e., length of arc AP = x We define cos x = a and sin x = b Since ∆OMP is a right triangle, we have OM2 … Read more