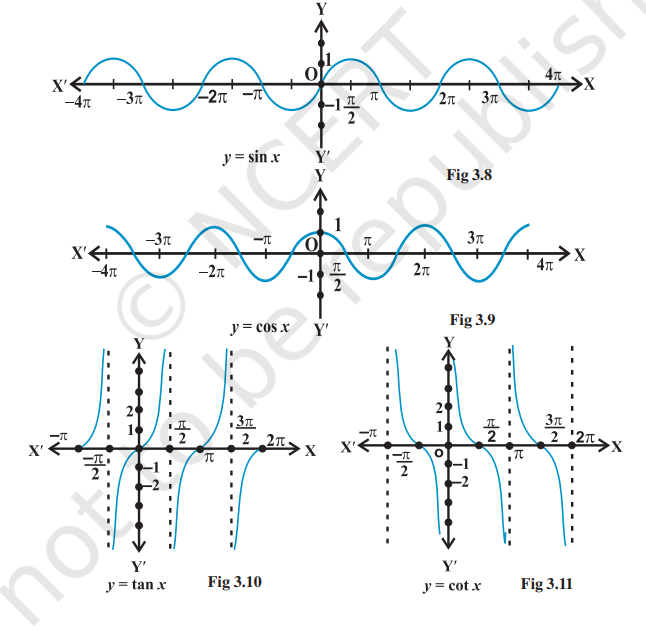
From the definition of sine and cosine functions, we observe that they are defined for all real numbers. Further, we observe that for each real number x,
– 1 ≤ sin x ≤ 1 and – 1 ≤ cos x ≤ 1
Thus, domain of y = sin x and y = cos x is the set of all real numbers and range is the interval [–1, 1], i.e., – 1 ≤ y ≤ 1
Since cosec x = 1 / sin x , the domain of y = cosec x is the set { x : x ∈ R and x ≠ n π, n ∈ Z} and range is the set {y : y ∈ R, y ≥ 1 or y ≤ – 1}. Similarly, the domain of y = sec x is the set {x : x ∈ R and x ≠ (2n + 1) π /2 , n ∈ Z} and range is the set {y : y ∈ R, y ≤ – 1or y ≥ 1}. The domain of y = tan x is the set {x : x ∈ R and x ≠ (2n + 1) π 2 , n ∈ Z} and range is the set of all real numbers. The domain of y = cot x is the set {x : x ∈ R and x ≠ n π, n ∈ Z} and the range is the set of all real numbers
We further observe that in the first quadrant, as x increases from 0 to π/ 2 , sin x increases from 0 to 1, as x increases from π /2 to π, sin x decreases from 1 to 0. In the third quadrant, as x increases from π to 3π/ 2 , sin x decreases from 0 to –1and finally, in the fourth quadrant, sin x increases from –1 to 0 as x increases from 3π/ 2 to 2π. Similarly, we can discuss the behaviour of other trigonometric functions. In fact, we have the following table:
| I quadrant | II quadrant | III quadrant | IV quadrant | |
| sin | increases from 0 to 1 | decreases from 1 to 0 | decreases from 0 to –1 | increases from –1 to 0 |
| cos | decreases from 1 to 0 | decreases from 0 to – 1 | increases from –1 to 0 | increases from 0 to 1 |
| tan | increases from 0 to ∞ | increases from –∞to 0 | increases from 0 to ∞ | increases from –∞to 0 |
| cot | decreases from ∞ to 0 | decreases from 0 to–∞ | decreases from ∞ to 0 | decreases from 0to –∞ |
| sec | increases from 1 to ∞ | increases from –∞to–1 | decreases from –1to–∞ | decreases from ∞ to 1 |
| cosec | decreases from ∞ to 1 | increases from 1 to ∞ | increases from –∞to–1 | decreases from–1to–∞ |
Remark In the above table, the statement tan x increases from 0 to ∞ (infinity) for 0 < x < π /2 simply means that tan x increases as x increases for 0 < x < π /2 and
assumes arbitraily large positive values as x approaches to π /2 . Similarly, to say that cosec x decreases from –1 to – ∞ (minus infinity) in the fourth quadrant means that cosec x decreases for x ∈ ( 3π /2 , 2π) and assumes arbitrarily large negative values as x approaches to 2π. The symbols ∞ and – ∞ simply specify certain types of behaviour of functions and variables
We have already seen that values of sin x and cos x repeats after an interval of 2π. Hence, values of cosec x and sec x will also repeat after an interval of 2π. We

Example If cos x = – 3 /5 , x lies in the third quadrant, find the values of other five trigonometric functions
Solution Since cos x = -3/5, we have sec x = -5 /3
sin2 x + cos2 x = 1, i.e., sin2 x = 1 – cos2 x
or sin2 x = 1 – 9 /25 = 16 /25
Hence sin x = ±4/5
Since x lies in third quadrant, sin x is negative. Therefore
sinx=-4/5
which also gives
cosec x = –5/4
Further, we have
tan x =sinx/cosx=4/3 and cotx=cosx/sinx =3/4
