Trigonometric Functions of Sum and Difference of Two Angles

The word ‘trigonometry’ is derived from the Greek words ‘trigon’ and ‘metron’ and it means ‘measuring the sides of a triangle’. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others. Currently, trigonometry is used in many areas such as the science of seismology, designing electric circuits, describing the state of an atom, predicting the heights of tides in the ocean, analysing a musical tone and in many other areas

trigonometric identities

• sin (– x) = – sin x
• cos (– x) = cos x
• cos (x + y) = cos x cos y – sin x sin y

Derivation of trigonometric identities

Consider the unit circle with centre at the origin. Let x be the angle P4OP1 and y be the angle P1OP2 . Then (x + y) is the angle P4OP2 . Also let (– y) be the angle P4OP3 . Therefore, P1 , P2 , P3 and P4 will have the coordinates P1 (cos x, sin x), P2 [cos (x + y), sin (x + y)], P3 [cos (– y), sin (– y)] and P4 (1, 0) (Fig 3.14)

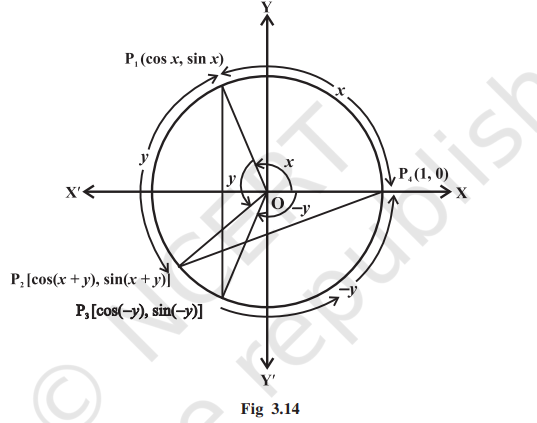
Consider the triangles P1OP3 and P2OP4 . They are congruent . Therefore, P1 P3 and P2 P4 are equal. By using distance formula, we get

P1 P3² = [cos x – cos (– y)]² + [sin x – sin(–y] ²

= (cos x – cos y) ²+ (sin x + sin y) ²

= cos² x + cos² y – 2 cos x cos y + sin² x + sin² y + 2sin x sin y

= 2 – 2 (cos x cos y – sin x sin y)

Also, P2 P4² = [1 – cos (x + y)] ² + [0 – sin (x + y)]²

= 1 – 2cos (x + y) + cos² (x + y) + sin² (x + y)

= 2 – 2 cos (x + y)

Since P1 P3 = P2 P4 , we have P1 P3 ² = P2 P4 ² .

Therefore, 2 –2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y).

Hence cos (x + y) = cos x cos y – sin x sin y

Others trigonometric identities

• cos (x – y) = cos x cos y + sin x sin y
• cos(π/2 -x ) = sin x
• sin(π/2 -x ) = cos x
• sin (x + y) = sin x cos y + cos x sin y
• sin (x – y) = sin x cos y – cos x sin y

tan (x + y) =(tan x + tan y)/(1-tan x tan y)

tan ( x – y)=(tanx – tany)/(1 + tan x tan y)

cot ( x + y)=(cotx coty – 1)/(cot + coty)

cot (x – y)=(cot x cot y + 1)/(cot y-cot x)

cos 2x= (1 – tan²x)/(1 + tan^2x)

sin2x=2tanx/(1 +tan²x)

tan2x=2tanx/(1-tan²x)

sin 3x = 3 sin x – 4 sin³ x

cos 3x= 4 cos³ x – 3 cos x

tan 3x =3tanx – tan³x/(1 – 3tan ²x)

cos x + cos y = 2 cos (x+y)/2 cos ( x- y)/2

cos x – cos y = –2 sin (x+y)/2 sin ( x- y)/2

sin x + sin y = 2 sin (x+y)/2 cos ( x- y)/2

sin x – sin y = 2 cos (x+y)/2 sin ( x- y)/2