Let P (a, b) be a point on the unit circle with centre at the origin such that ∠AOP = x. If ∠AOQ = – x, then the coordinates of the point Q will be (a, –b) . Therefore
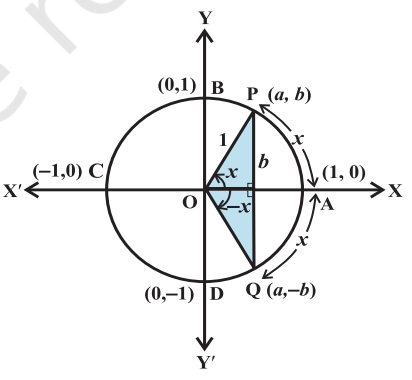
cos (– x) = cos x
and sin (– x) = – sin x
Since for every point P (a, b) on the unit circle, – 1 ≤ a ≤ 1 and – 1 ≤ b ≤ 1, we have – 1 ≤ cos x ≤ 1 and –1 ≤ sin x ≤ 1 for all x.
in the first quadrant (0 < x < π 2 ) a and b are both positive,
in the second quadrant ( π /2 < x < π) a is negative and b is positive,
in the third quadrant (π < x <3π/2) a and b are both negative
in the fourth quadrant ( 3π /2 < x < 2π) a is positive and b is negative
Therefore, sin x is positive for 0 < x < π, and negative for π < x < 2π
Similarly, cos x is positive for 0 < x < π 2 , negative for π 2 < x < 3π 2 and also positive for 3π/ 2 < x < 2π.
| I | II | III | IV | |
|---|---|---|---|---|
| sin x | + | + | – | – |
| cos x | + | – | – | + |
| tan x | + | – | + | – |
| cosec x | + | + | – | – |
| sec x | + | – | – | + |
| cot x | + | – | + | – |
