Coordinate Geometry, also known as Cartesian Geometry or Analytic Geometry, is a branch of mathematics that merges algebraic techniques with geometric intuition. It provides a powerful framework for representing geometric shapes and solving problems by introducing coordinates to the geometric objects.
The Cartesian Coordinate System

The cornerstone of coordinate geometry is the Cartesian Coordinate System, developed by René Descartes. It consists of two perpendicular axes, the x-axis, and the y-axis, intersecting at a point called the origin (0, 0).
The position of a point in the plane is specified by an ordered pair of numbers (x, y), where x represents the horizontal distance along the x-axis, and y represents the vertical distance along the y-axis. This system allows us to precisely define and analyze geometric shapes.
Equation of a Line
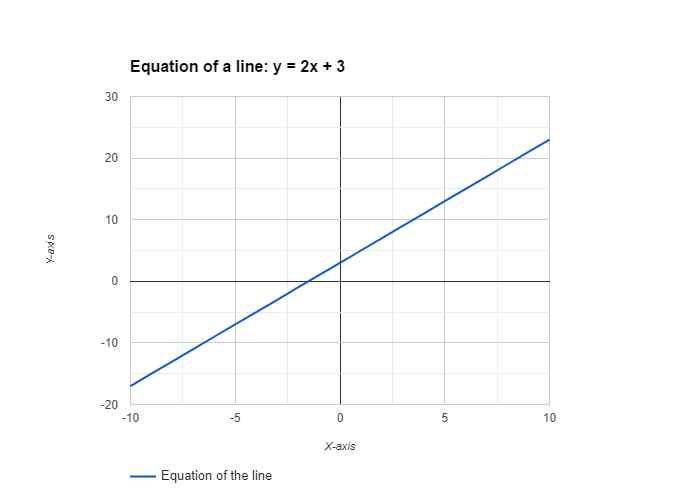
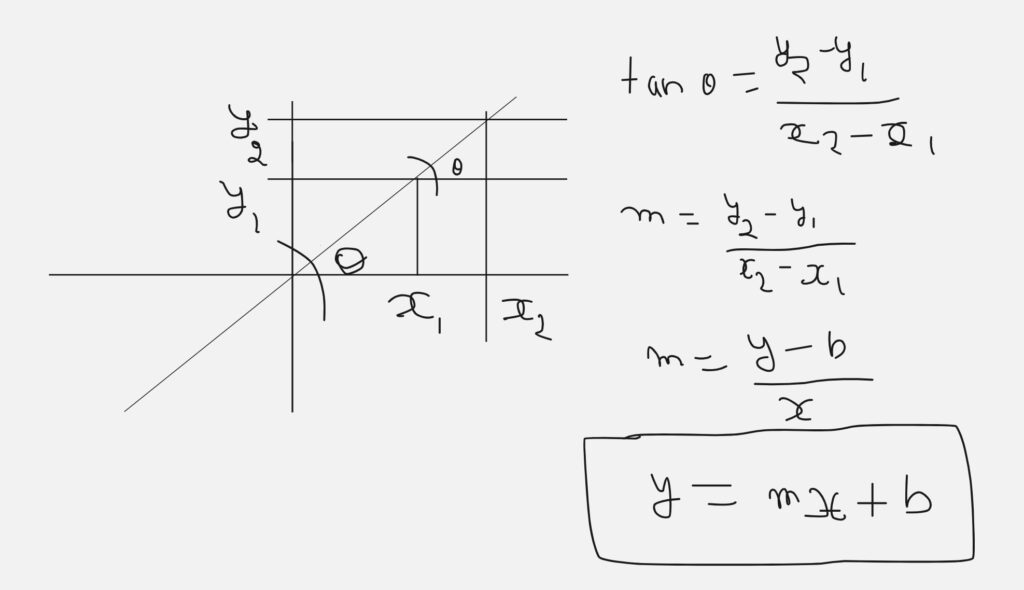
The equation of a line in the Cartesian Coordinate System is often expressed in the form y = mx + b, where:
mis the slope of the line, indicating the rate of change.bis the y-intercept, the point where the line crosses the y-axis.
For example, consider a line with a slope of 2 and a y-intercept of 3:y = 2x + 3
This equation tells us that for every unit increase in x, the corresponding y value increases by 2, and the line crosses the y-axis at the point (0, 3).
Distance Formula
The distance between two points (x1, y1) and (x2, y2) in a Cartesian plane can be calculated using the distance formula:d = √((x2 - x1)² + (y2 - y1)²)
For instance, to find the distance between points (3, 4) and (6, 8):d = √((6 - 3)² + (8 - 4)²)
Calculating this gives us the distance d = √(9 + 16) = √25 = 5.
Midpoint Formula
The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) can be found using the midpoint formula:((x1 + x2)/2, (y1 + y2)/2)
For example, the midpoint of the line segment with endpoints (2, 3) and (6, 9) is:((2 + 6)/2, (3 + 9)/2) = (4, 6)
Coordinate Geometry, a branch of mathematics rooted in the Cartesian Coordinate System, reaches beyond the basics to explore advanced concepts that deepen our understanding of geometric relationships and analytical techniques.
Polar Coordinates
In addition to the Cartesian Coordinate System, there is another coordinate system known as Polar Coordinates. In polar coordinates, a point is represented by an angle (θ) and a distance (r) from the origin. The conversion between Cartesian and polar coordinates involves trigonometric functions.
For example, the Cartesian point (x, y) can be expressed in polar coordinates as (r, θ) where r = √(x² + y²) and θ = arctan(y/x).
Parametric Equations
Parametric equations describe the coordinates of a point as functions of an independent variable, often denoted as t. The motion of objects, curves, and complex shapes can be precisely defined using parametric equations. For instance, a parametric representation of a circle can be given by:
x = r * cos(t)y = r * sin(t)
Here, r is the radius of the circle, and t varies from 0 to 2π to complete a full circle.
Transformations in the Coordinate Plane
Coordinate Geometry extends into the realm of transformations, allowing us to manipulate and visualize shapes in the plane. Translation, rotation, scaling, and reflection are fundamental transformations that alter the position, orientation, and size of geometric figures.
For example, a translation of a point (x, y) by (a, b) can be represented as:
x' = x + ay' = y + b
Advanced Applications: Differential Geometry
Differential Geometry delves into the study of curves and surfaces using calculus. Concepts like curvature, tangent vectors, and normal vectors provide a deeper understanding of the geometric properties of curves and surfaces. Differential geometry plays a crucial role in various scientific and engineering fields.
Conclusion
Coordinate Geometry, with its advanced topics such as polar coordinates, parametric equations, transformations, and differential geometry, elevates mathematical exploration to new heights. By integrating algebraic techniques with geometric insights, mathematicians unlock the potential to model complex phenomena, visualize intricate shapes, and solve problems across diverse domains.
