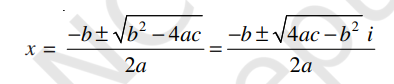Let us denote √−1 by the symbol i . Then, we have i2 = −1 . This means that i is a solution of the equation x2 + 1 = 0
A number of the form a + ib, where a and b are real numbers, is defined to be a complex number
For example, 2 + i3, (– 1) + i√3 , 4 + i(-1/11) are complex numbers
For the complex number z = a + ib, a is called the real part, denoted by Re z and b is called the imaginary part denoted by Im z of the complex number z. For example, if z = 2 + i5, then Re z = 2 and Im z = 5.
Two complex numbers z1 = a + ib and z2 = c + id are equal if a = c and b = d
Example If 4x + i(3x – y) = 3 + i (– 6), where x and y are real numbers, then find
the values of x and y.
Solution We have
4x + i (3x – y) = 3 + i (–6) … (1)
Equating the real and the imaginary parts of (1), we get
4x = 3, 3x – y = – 6,
which, on solving simultaneously, give x=3/4 and y=33/4
Algebra of Complex Numbers
Addition of two complex numbers Let z1 = a + ib and z2=c + id be any two complex numbers Then, the sum z1 + z2 is defined as follows:
z1 + z2 = (a + c) + i(b + d), which is again a complex number
For example, (2 + i3) + (– 6 +i5) = (2 – 6) + i(3 + 5) = – 4 + i8
The addition of complex numbers satisfy the following properties:
(i) The closure law The sum of two complex numbers is a complex number, i.e., z1 + z2 is a complex number for all complex numbers z1 and z2
(ii) The commutative law z1 + z2 = z2 + z1
iii) The associative law z1 + ( z2 + z3 ) = (z1 + z2 ) + z3
(iv) The existence of additive identity There exists the complex number 0 + i 0 (denoted as 0), called the additive identity or the zero complex number, such that, for every complex number z, z + 0 = z.
(v) The existence of additive inverse To every complex number z = a + ib, we have the complex number – a + i(– b) (denoted as – z), called the additive inverse or negative of z. We observe that z + (–z) = 0 (the additive identity)
Difference of two complex numbers
z1 – z2 = z1 + (-z2 )
For example, (6 + 3i) – (2 – i) = (6 + 3i) + (– 2 + i ) = 4 + 4i
and (2 – i) – (6 + 3i) = (2 – i) + ( – 6 – 3i) = – 4 – 4i
Multiplication of two complex numbers Let z1= a +ib and z2 = c +id be any two complex numbers. Then, the product z1 z2 is defined as follows:
z1z2= (ac – bd) + i(ad + bc)
For example, (3 + i5) (2 + i6) = (3 × 2 – 5 × 6) + i(3 × 6 + 5 × 2) = – 24 + i28
The multiplication of complex numbers possesses the following properties, which we state without proofs.
(i) The closure law The product of two complex numbers is a complex number, the product z1 z2 is a complex number for all complex numbers z1 and z2
(ii) The commutative law For any two complex numbers z1 and z2 ,
z1 z2 = z2 z1 .
(iii) The associative law (z1 z2 ) z3 = z1 (z2 z3 ).
(iv) The existence of multiplicative identity There exists the complex number 1 + i 0 (denoted as 1), called the multiplicative identity such that z.1 = z, for every complex number z
(v) The existence of multiplicative inverse For every non-zero complex number z = a + ib or a + bi(a ≠ 0, b ≠ 0), we have the complex number
a/(a2 + b2) + i(-b)/(a2 + b2)
(denoted by 1/z or z-1 ) , called the multiplicative inverse of z such that
z.1/z= 1
(vi) The distributive law For any three complex numbers z1 , z2 , z3 ,
(a) z1 (z2 + z3 ) = z1 z2 + z1 z3
(b) (z1 + z2 ) z 3 = z1 z3 + z2 z3
Division of two complex numbers
Given any two complex numbers z1 and z2 , where z2 ≠ 0 , the quotient z1/z2 is defined by
z1/z2=z1 1/z2
Power of i we know that
In general, for any integer k, i4k =1 , i4k + 1 = i , i4k + 2 = -1, i4k + 3 = -i
The Modulus and the Conjugate of a Complex Number
Let z = a + ib be a complex number. Then, the modulus of z, denoted by | z |, is defined to be the non-negative real number
√a2 + b2= i.e., | z | = √ a2 + b2 and the conjugate of z, denoted as z̄ , is the complex number a – ib, i.e., z = a – ib.
Argand Plane and Polar Representation
We already know that corresponding to each ordered pair of real numbers (x, y), we get a unique point in the XY-plane and vice-versa with reference to a set of mutually perpendicular lines known as the x-axis and the y-axis. The complex number x + iy which corresponds to the ordered pair (x, y) can be represented geometrically as the unique point P(x, y) in the XY-plane and vice-versa.
Some complex numbers such as 2 + 4i, – 2 + 3i, 0 + 1i, 2 + 0i, – 5 –2i and 1 – 2i which correspond to the ordered pairs (2, 4), ( – 2, 3), (0, 1), (2, 0), ( –5, –2), and (1, – 2), respectively, have been represented geometrically by the points A, B, C, D, E, and F, respectively in the Fig 5.1.
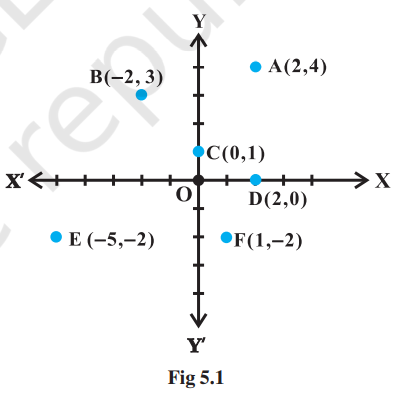
The plane having a complex number assigned to each of its point is called the complex plane or the Argand plane.
Obviously, in the Argand plane, the modulus of the complex number x + iy = √ x2 + y2 is the distance between the point P(x, y) and the origin O (0, 0) (Fig 5.2). The points on the x-axis corresponds to the complex numbers of the form a + i 0 and the points on the y-axis corresponds to the complex numbers of the form
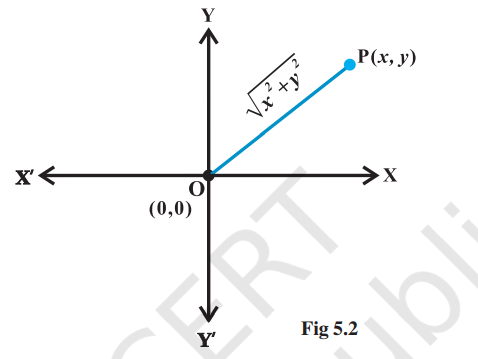
0 + ib. The x-axis and y-axis in the Argand plane are called, respectively, the real axis and the imaginary axis
The representation of a complex number z = x + iy and its conjugate z = x – iy in the Argand plane are, respectively, the points P (x, y) and Q (x, – y).
Geometrically, the point (x, – y) is the mirror image of the point (x, y) on the real axis (Fig 5.3).

Polar representation of a complex number
Let the point P represent the non-zero complex number z = x + iy. Let the directed line segment OP be of length r and θ be the angle which OP makes with the positive direction of x-axis (Fig 5.4)
We may note that the point P is uniquely determined by the ordered pair of real numbers (r, θ), called the polar coordinates of the point P. We consider the origin as the pole and the positive direction of the x axis as the initial line.
We have, x = r cos θ, y = r sin θ and therefore, z = r (cos θ + i sin θ). The latter is said to be the polar form of the complex number. Here r=√ x2 + y2 = is the modulus of z and θ is called the argument (or amplitude) of z which is denoted by arg z
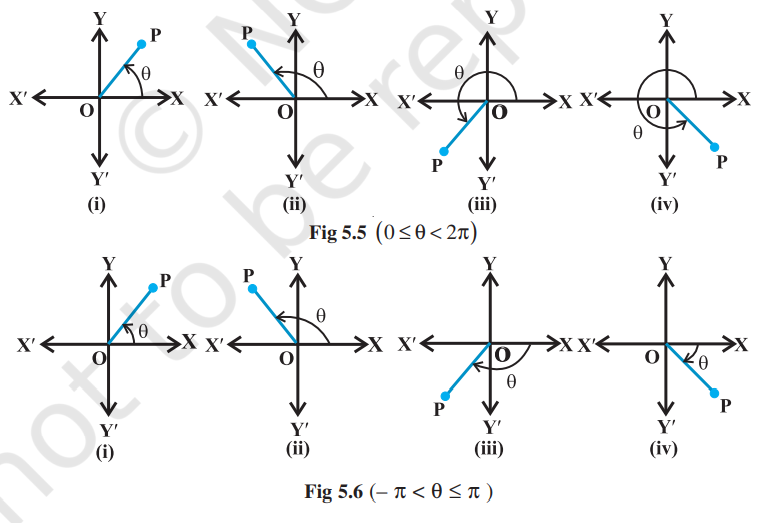
For any complex number z ≠ 0, there corresponds only one value of θ in 0 ≤ θ < 2π. However, any other interval of length 2π, for example – π < θ ≤ π, can be such an interval.We shall take the value of θ such that – π < θ ≤ π, called principal argument of z and is denoted by arg z, unless specified otherwise. (Figs. 5.5 and 5.6)
Quadratic Equations
We are already familiar with the quadratic equations and have solved them in the set of real numbers in the cases where discriminant is non-negative, i.e., ≥ 0,
Let us consider the following quadratic equation:
ax2 + bx + c = 0 with real coefficients a, b, c and a ≠ 0.
Also, let us assume that the b2 – 4ac < 0.
Now, we know that we can find the square root of negative real numbers in the set of complex numbers. Therefore, the solutions to the above equation are available in the set of complex numbers which are given by