The principal source of noise in digital images arises during image acquisition and /or transmission. The performance of imaging sensors is affected by a variety of factors, such as environmental conditions during image acquisition and by the quality of the sensing elements themselves. Images are corrupted during transmission principally due to interference in the channels used for transmission. Since main sources of noise presented in digital images are resulted from atmospheric disturbance and image sensor circuitry, following assumptions can be made i.e. the noise model is spatial invariant (independent of spatial location). The noise model is uncorrelated with the object function
Gaussian Noise:
These noise models are used frequently in practices because of its tractability in both spatial and frequency domain. The PDF of Gaussian random variable is as follows, where z represents the gray level, μ= mean of average value 0
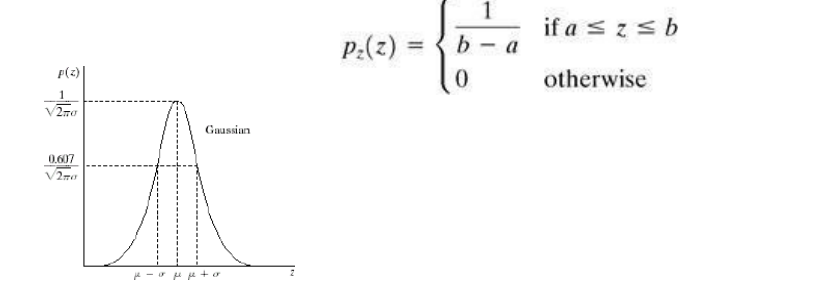
Rayleigh Noise:
Unlike Gaussian distribution, the Rayleigh distribution is no symmetric. It is given by the formula.
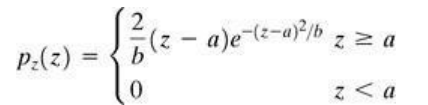
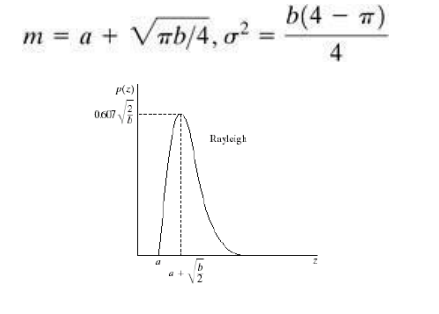
The mean and variance of this density is
Gamma Noise
The PDF of Erlang noise is given by
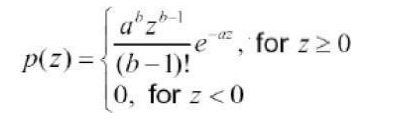
The mean and variance of this density are given by
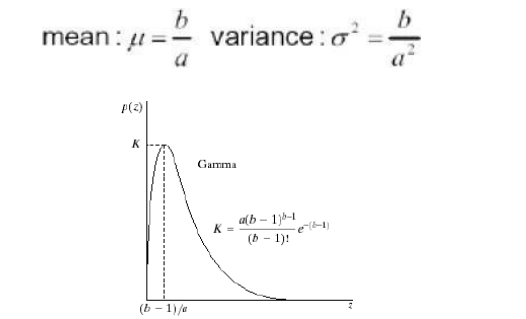
Its shape is similar to Rayleigh disruption. This equation is referred to as gamma density it is correct only when the denominator is the gamma function.
Exponential Noise:
Exponential distribution has an exponential shape. The PDF of exponential noise is given as
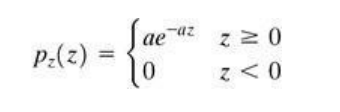
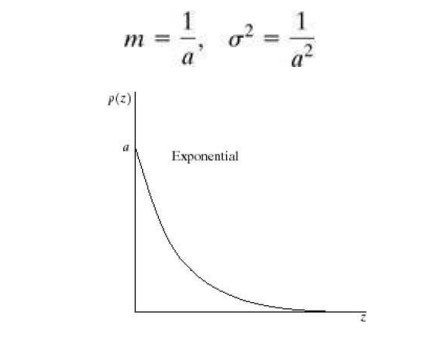
Where a>0. The mean and variance of this density are given by
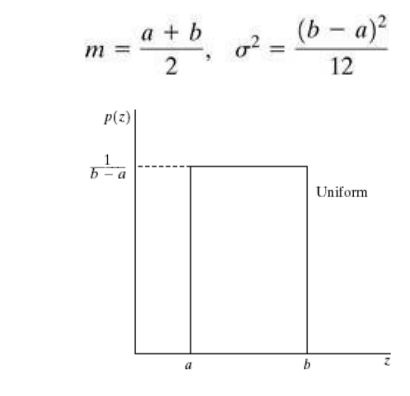
Uniform Noise:
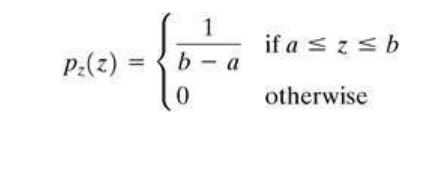
The mean and variance of this noise is
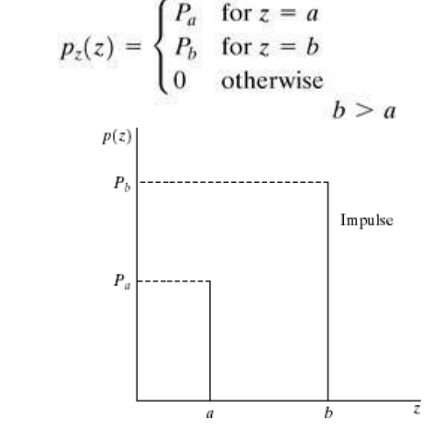
Impulse (Salt &Pepper) Noise:
In this case, the noise is signal dependent, and is multiplied to the image. The PDF of bipolar (impulse) noise is given by If b>a, gray level b will appear as a light dot in image. Level a will appear like a dark dot
Restoration in the Presence of Noise Only- Spatial Filtering:
When the only degradation present in an image is noise, i.e.
g(x,y)=f(x,y)+η(x,y)
or
G(u,v)= F(u,v)+ N(u,v)
The noise terms are unknown so subtracting them from g(x,y) or G(u,v) is not a realistic approach. In the case of periodic noise it is possible to estimate N(u,v) from the spectrum G(u,v).So, N(u,v) can be subtracted from G(u,v) to obtain an estimate of original image. Spatial filtering can be done when only additive noise is present. The following techniques can be used to reduce the noise effect
