Restoration improves image in some predefined sense. It is an objective process. Restoration attempts to reconstruct an image that has been degraded by using a priori knowledge of the degradation phenomenon. These techniques are oriented toward modeling the degradation and then applying the inverse process in order to recover the original image. Restoration techniques are based on mathematical or probabilistic models of image processing. Enhancement, on the other hand is based on human subjective preferences regarding what constitutes a “good” enhancement result. Image Restoration refers to a class of methods that aim to remove or reduce the degradations that have occurred while the digital image was being obtained. All-natural images when displayed have gone through some sort of degradation:
- During display mode
- . Acquisition mode, or
- Processing mode
- Sensor noise
- Blur due to camera mis focus
- Relative object-camera motion
- Random atmospheric turbulence
- Others
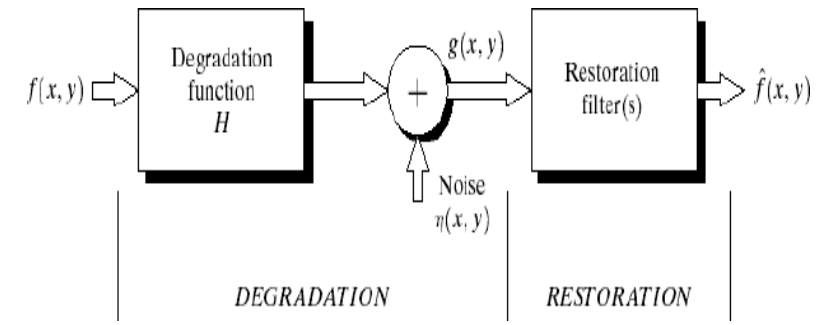
DEGRADATION MODEL:
Degradation process operates on a degradation function that operates on an input image with an additive noise term. Input image is represented by using the notation f(x,y), noise term can be represented as η(x,y).These two terms when combined gives the result as g(x,y). If we are given g(x,y), some knowledge about the degradation function H or J and some knowledge about the additive noise teem η(x,y), the objective of restoration is to obtain an estimate f'(x,y) of the original image. We want the estimate to be as close as possible to the original image. The more we know about h and η , the closer f(x,y) will be to f'(x,y). If it is a linear position invariant process, then degraded image is given in the spatial domain by
g(x,y)=f(x,y)*h(x,y)+η(x,y)
where h(x,y) is spatial representation of degradation function and symbol * represents convolution. In frequency domain we may write this equation as
G(u,v)=F(u,v)H(u,v)+N(u,v)
The terms in the capital letters are the Fourier Transform of the corresponding terms in the spatial domain.