An abstraction is a mechanism for separating the properties of an object and restricting the focus to those relevant in the current context. The user of the abstraction does not have to understand all of the details in order to utilize the object, but only those relevant to the current task or problem.
Two common types of abstractions encountered in computer science are procedural, or functional, abstraction and data abstraction. Procedural abstraction is the use of a function or method knowing what it does but ignoring how it’s accomplished.
Consider the mathematical square root function which you have probably used at some point. You know the function will compute the square root of a given number, but do you know how the square root is computed ?
Typically, abstractions of complex problems occur in layers, with each higher layer adding more abstraction than the previous. Consider the problem of representing integer values on computers and performing arithmetic operations on those values. Given below illustrates the common levels of abstractions used with integer arithmetic. At the lowest level is the hardware with little to no abstraction since it includes binary representations of the values and logic circuits for performing the arithmetic.
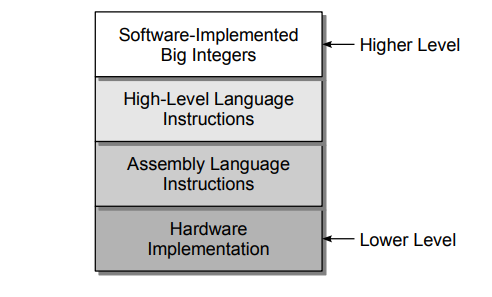
Hardware designers would deal with integer arithmetic at this level and be concerned with its correct implementation. A higher level of abstraction for integer values and arithmetic is provided through assembly language, which involves working with binary values and individual instructions corresponding to the underlying hardware.
Compiler writers and assembly language programmers would work with integer arithmetic at this level and must ensure the proper selection of assembly language instructions to compute a given mathematical expression. For example, suppose we wish to compute x = a + b − 5. At the assembly language level, this expression must be split into multiple instructions for loading the values from memory, storing them into registers, and then performing each arithmetic operation separately, as shown in the following psuedocode:
