Every node in a binary search tree contains one value and two pointers, left and right, which point to the node’s left and right sub-trees, respectively. The structure of a binary search tree node is shown

The same concept is used in an M-way search tree which has M – 1 values per node and M sub trees. In such a tree, M is called the degree of the tree. Note that in a binary search tree M = 2, so it has one value and two sub-trees. In other words, every internal node of an M-way search tree consists of pointers to M sub-trees and contains M – 1 keys, where M > 2. The structure of an M-way search tree node is shown in Fig. 11.2.

In the structure shown, P0 , P1 , P2 , …, Pn are pointers to the node’s sub-trees and K0 , K1 , K2 , …, Kn–1 are the key values of the node. All the key values are stored in ascending order. That is, Ki < Ki+1 for 0 < i < n–2.
In an M-way search tree, it is not compulsory that every node has exactly M–1 values and M sub trees. Rather, the node can have anywhere from 1 to M–1 values, and the number of sub-trees can vary from 0 (for a leaf node) to i + 1, where i is the number of key values in the node. M is thus a fixed upper limit that defines how many key values can be stored in the node.
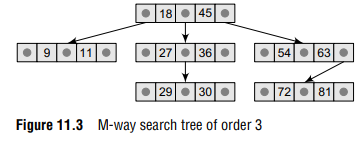
Consider the M-way search tree shown in Fig. 11.3. Here M = 3. So a node can store a maximum of two key values and can contain pointers to three sub-trees. In our example, we have taken a very small value of M so that the concept becomes easier for the reader, but in practice, M is usually very large. Using a 3-way search tree, let us lay down some of the basic properties of an M-way search tree.
- Note that the key values in the sub-tree pointed by P0 are less than the key value K0 . Similarly, all the key values in the sub-tree pointed by P1 are less than K1 , so on and so forth. Thus, the generalized rule is that all the key values in the sub-tree pointed by Pi are less than Ki , where 0 ≤ i ≤ n–1.
- Note that the key values in the sub-tree pointed by P1 are greater than the key value K0 . Similarly, all the key values in the sub-tree pointed by P2 are greater than K1 , so on and so forth. Thus, the generalized rule is that all the key values in the sub-tree pointed by Pi are greater than Ki–1, where 0 ≤ i ≤ n–1.
In an M-way search tree, every sub-tree is also an M-way search tree and follows the same rules.
