When we access a node N, splaying is performed on N to move it to the root. To perform a splay operation, certain splay steps are performed where each step moves N closer to the root. Splaying a particular node of interest after every access ensures that the recently accessed nodes are kept closer to the root and the tree remains roughly balanced, so that the desired amortized time bounds can be achieved.
Each splay step depends on three factors:
- Whether N is the left or right child of its parent P,
- Whether P is the root or not, and if not,
- Whether P is the left or right child of its parent, G (N’s grandparent).
Depending on these three factors, we have one splay step based on each factor
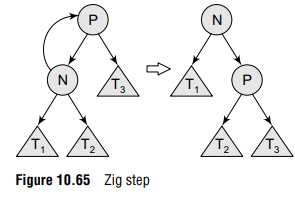
Zig step The zig operation is done when P (the parent of N) is the root of the splay tree. In the zig step, the tree is rotated on the edge between N and P. Zig step is usually performed as the last step in a splay operation and only when N has an odd depth at the beginning of the operation. Refer Fig. 10.65
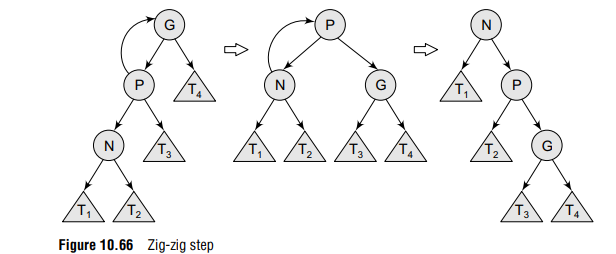
Zig-zig step The zig–zig operation is performed when P is not the root. In addition to this, N and P are either both right or left children of their parents. Figure 10.66 shows the case where N and P are the left children. During the zig–zig step, first the tree is rotated on the edge joining P and its parent G, and then again rotated on the edge joining N and P.
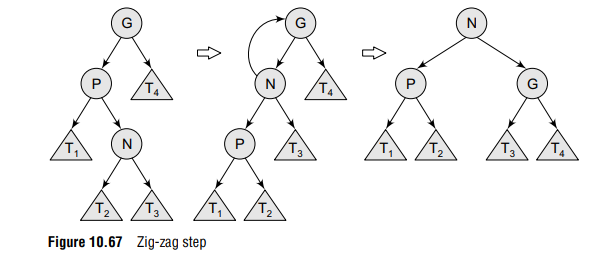
Zig-zag step The zig–zag operation is performed when P is not the root. In addition to this, N is the right child of P and P is the left child of G or vice versa. In zig–zag step, the tree is first rotated on the edge between N and P, and then rotated on the edge between N and G. Refer Fig.10.67.
Inserting a Node in a Splay Tree
Although the process of inserting a new node N into a splay tree begins in the same way as we insert a node in a binary search tree, but after the insertion, N is made the new root of the splay tree. The steps performed to insert a new node N in a splay tree can be given as follows:
Step 1 Search N in the splay tree. If the search is successful, splay at the node N
Step 2 If the search is unsuccessful, add the new node N in such a way that it replaces the NULL pointer reached during the search by a pointer to a new node N. Splay the tree at N.
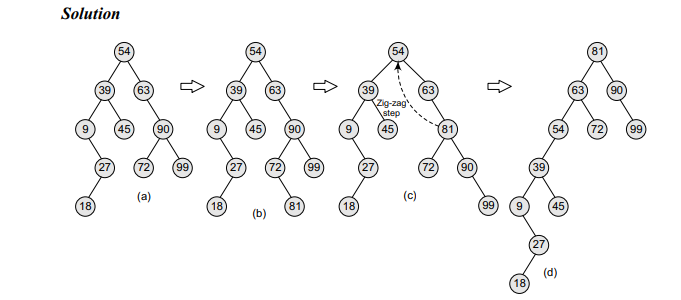
Example 10.11 Consider the splay tree given on the left. Observe the change in its structure when 81 is added to it.
Advantages and Disadvantages of Splay Trees
The advantages of using a splay tree are:
- A splay tree gives good performance for search, insertion, and deletion operations. This advantage centres on the fact that the splay tree is a self-balancing and a self-optimizing data structure in which the frequently accessed nodes are moved closer to the root so that they can be accessed quickly. This advantage is particularly useful for implementing caches and garbage collection algorithms.
- Splay trees are considerably simpler to implement than the other self-balancing binary search trees, such as red-black trees or AVL trees, while their average case performance is just as efficient.
- Splay trees minimize memory requirements as they do not store any book-keeping data
- Unlike other types of self-balancing trees, splay trees provide good performance (amortized O(log n)) with nodes containing identical keys.
However, the demerits of splay trees include:
- While sequentially accessing all the nodes of a tree in a sorted order, the resultant tree becomes completely unbalanced. This takes n accesses of the tree in which each access takes O(log n) time. For example, re-accessing the first node triggers an operation that in turn takes O(n) operations to rebalance the tree before returning the first node. Although this creates a significant delay for the final operation, the amortized performance over the entire sequence is still O(log n).
- For uniform access, the performance of a splay tree will be considerably worse than a somewhat balanced simple binary search tree. For uniform access, unlike splay trees, these other data structures provide worst-case time guarantees and can be more efficient to use.
