The word ‘trigonometry’ is derived from the Greek words ‘trigon’ and ‘metron’ and it means ‘measuring the sides of a triangle’. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others. Currently, trigonometry is used in many areas such as the science of seismology, designing electric circuits, describing the state of an atom, predicting the heights of tides in the ocean, analysing a musical tone and in many other areas
Angles
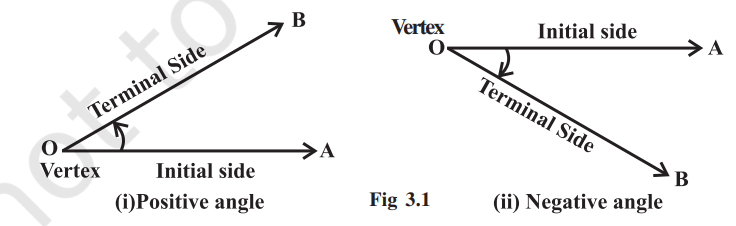
Angle is a measure of rotation of a given ray about its initial point. The original ray is called the initial side and the final position of the ray after rotation is called the terminal side of the angle. The point of rotation is called the vertex. If the direction of rotation is anticlockwise, the angle is said to be positive and if the direction of rotation is clockwise, then the angle is negative
Degree measure
If a rotation from the initial side to terminal side is (1/360)th of a revolution, the angle is said to have a measure of one degree, written as 1°. A degree is divided into 60 minutes, and a minute is divided into 60 seconds . One sixtieth of a degree is called a minute, written as 1′, and one sixtieth of a minute is called a second, written as 1″. Thus, 1° = 60′, 1′ = 60″
Some of the angles whose measures are 360°,180°, 270°, 420°, – 30°, – 420° are shown

Radian measure
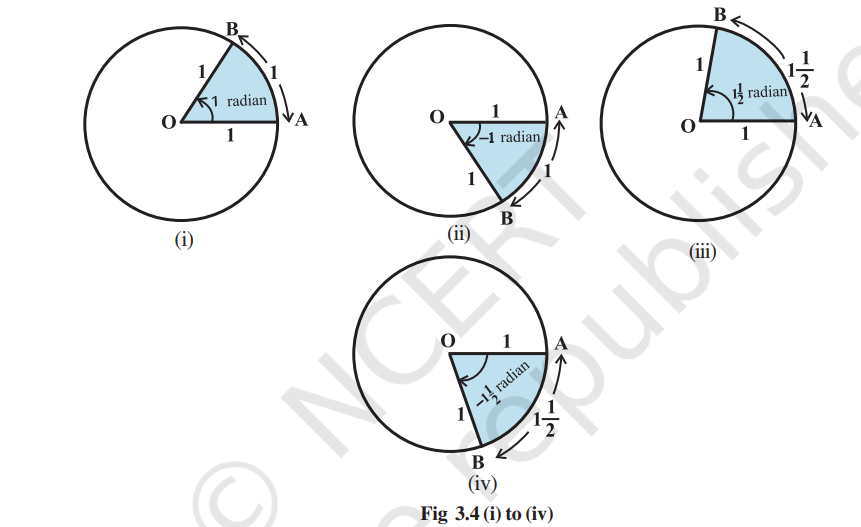
There is another unit for measurement of an angle, called the radian measure. Angle subtended at the centre by an arc of length 1 unit in a unit circle (circle of radius 1 unit) is said to have a measure of 1 radian. In the Fig 3.4(i) to (iv), OA is the initial side and OB is the terminal side.
The figures show the angles whose measures are 1 radian, –1 radian, 11/2 radian and -11/2 radian
We know that the circumference of a circle of radius 1 unit is 2π. Thus, one complete revolution of the initial side subtends an angle of 2π radian
More generally, in a circle of radius r, an arc of length r will subtend an angle of 1 radian. It is well-known that equal arcs of a circle subtend equal angle at the centre. Since in a circle of radius r, an arc of length r subtends an angle whose measure is 1 radian, an arc of length l will subtend an angle whose measure is l / r radian. Thus, if in a circle of radius r, an arc of length l subtends an angle θ radian at the centre, we have θ = l / r or l = r θ
Relation between degree and radian
Since a circle subtends at the centre an angle whose radian measure is 2π and its degree measure is 360°, it follows that
2π radian = 360° or π radian = 180°
The above relation enables us to express a radian measure in terms of degree measure and a degree measure in terms of radian measure. Using approximate value of π as 22 / 7 , we have
1 radian = 180 / π ° = 57° 16′ approximately. Also 1° = π /180 radian = 0.01746 radian approximately
The relation between degree measures and radian measure of some common angles are given in the following table:
| Degree | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radian | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
Notational Convention
Since angles are measured either in degrees or in radians, we adopt the convention that whenever we write angle θ°, we mean the angle whose degree measure is θ and whenever we write angle β, we mean the angle whose radian measure is β.
Note that when an angle is expressed in radians, the word ‘radian’ is frequently omitted. Thus, π= 180 and π/4=45° are written with the understanding that π and π / 4 are radian measures. Thus, we can say that
Radian measure = π / 180 × Degree measure
Degree measure = 180 / π ×Radian measure
Example Convert 40° 20′ into radian measure
Solution We know that 180° = π radian.
Hence 40° 20′ = 40 1/3 degree = π /180 × 121 / 3 radian = 121π / 540 radian
Trigonometric Functions
Consider a unit circle with centre at origin of the coordinate axes. Let P (a, b) be any point on the circle with angle AOP = x radian, i.e., length of arc AP = x

We define cos x = a and sin x = b Since ∆OMP is a right triangle, we have OM2 + MP2 = OP2 or a2 + b2 = 1 Thus, for every point on the unit circle, we have a2 + b2 = 1 or cos2 x + sin2 x = 1 Since one complete revolution subtends an angle of 2π radian at the centre of the circle, ∠AOB = π / 2
∠AOC = π and ∠AOD = 3π 2 . All angles which are integral multiples of π / 2 are called quadrantal angles. The coordinates of the points A, B, C and D are, respectively, (1, 0), (0, 1), (–1, 0) and (0, –1). Therefore, for quadrantal angles, we have
cos 0° = 1 sin 0° = 0,
cosπ / 2 = 0 sinπ / 2 = 1
cosπ = − 1 sinπ = 0
cos3π/ 2 = 0 sin3π / 2 = –1
cos 2π = 1 sin 2π = 0
Now, if we take one complete revolution from the point P, we again come back to same point P. Thus, we also observe that if x increases (or decreases) by any integral multiple of 2π, the values of sine and cosine functions do not change. Thus
sin (2nπ + x) = sin x, n ∈ Z , cos (2nπ + x) = cos x , n ∈ Z
Further, sin x = 0, if x = 0, ± π, ± 2π , ± 3π, …, i.e., when x is an integral multiple of π and cos x = 0, if x = ± π / 2 , ± 3π/ 2 , ± 5π /2 , … i.e., cos x vanishes when x is an odd multiple of π/ 2 . Thus
sin x = 0 implies x = nπ, where n is any integer
cos x = 0 implies x = (2n + 1) π / 2 , where n is any integer.
other trigonometric functions
cosec x = 1/ sin x , x ≠ nπ, where n is any integer
sec x = 1 /cos x , x ≠ (2n + 1) π /2 , where n is any integer
tan x = sinx /cos x , x ≠ (2n +1) π /2 , where n is any integer.
cot x = cosx / sinx , x ≠ n π, where n is any integer
We have shown that for all real x, sin2 x + cos2 x = 1
1 + tan2 x = sec2 x
1 + cot2 x = cosec2 x
Table of values of trigonometric ratios for 0°, 30°, 45°, 60° and 90°
| 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
|---|---|---|---|---|---|---|---|---|
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | undefined | 0 | undefined | 0 |
