A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B
In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element
If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f.
The function f from A to B is denoted by f: A → B
Example Let N be the set of natural numbers and the relation R be defined on
N such that R = {(x, y) : y = 2x, x, y ∈ N}.
What is the domain, codomain and range of R? Is this relation a function?
Solution The domain of R is the set of natural numbers N. The codomain is also N.
The range is the set of even natural numbers.
Since every natural number n has one and only one image, this relation is a
function
Example Examine each of the following relations given below and state in each
case, giving reasons whether it is a function or not?
(i) R = {(2,1),(3,1), (4,2)}, (ii) R = {(2,2),(2,4),(3,3), (4,4)}
(iii) R = {(1,2),(2,3),(3,4), (4,5), (5,6), (6,7)}
Solution (i) Since 2, 3, 4 are the elements of domain of R having their unique images,
this relation R is a function.
(ii) Since the same first element 2 corresponds to two different images 2
and 4, this relation is not a function.
(iii) Since every element has one and only one image, this relation is a
function
Types of function and their graphs
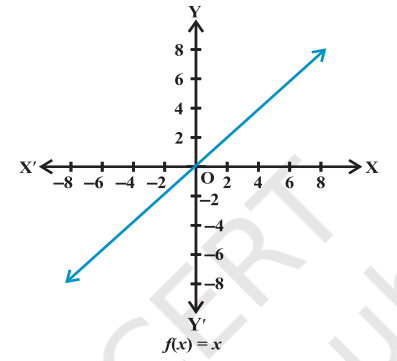
Identity function Let R be the set of real numbers. Define the real valued function f : R → R by y = f(x) = x for each x ∈ R. Such a function is called the identity function. Here the domain and range of f are R.
Graph of identity function
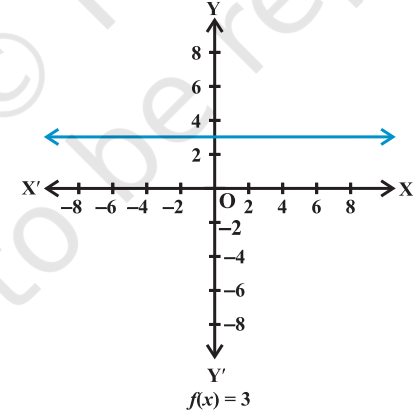
Constant function Define the function f: R → R by y = f (x) = c, x ∈ R where c is a constant and each x ∈ R. Here domain of f is R and its range is {c}.
Polynomial function A function f : R → R is said to be polynomial function if for each x in R, y = f (x) = a0 + a1 x + a2 x2 + …+ an xn , where n is a non-negative integer and a0 , a1 , a2 ,…,an ∈R
functions defined by f(x) = x3 – x3 + 2 is Polynomial function
