A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A × B. The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in A × B. The second element is called the image of the first element.
The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R
The set of all second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the codomain of the relation R. Note that range ⊂ codomain
Keys points of Relations
- A relation may be represented algebraically either by the Roster method or by the Set-builder method
- An arrow diagram is a visual representation of a relation
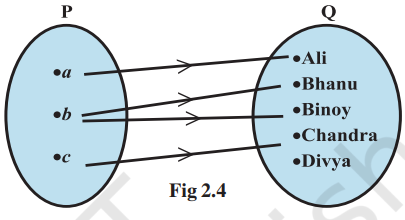
Consider the two sets P = {a, b, c} and Q = {Ali, Bhanu, Binoy, Chandra, Divya}. The cartesian product of P and Q has 15 ordered pairs which can be listed as P × Q = {(a, Ali), (a,Bhanu), (a, Binoy), …, (c, Divya)}
We can now obtain a subset of P × Q by introducing a relation R between the first element x and the second element y of each ordered pair (x, y) as
R= { (x,y): x is the first letter of the name y, x ∈ P, y ∈ Q}. Then R = {(a, Ali), (b, Bhanu), (b, Binoy), (c, Chandra)} A visual representation of this relation R (called an arrow diagram) is shown in Fig 2.4
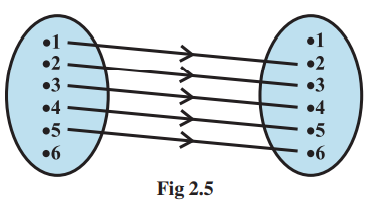
Example Let A = {1, 2, 3, 4, 5, 6}. Define a relation R from A to A by
R = {(x, y) : y = x + 1 }
(i) Depict this relation using an arrow diagram.
(ii) Write down the domain, codomain and range of R
Solution (i) By the definition of the relation,
R = {(1,2), (2,3), (3,4), (4,5), (5,6)}
The corresponding arrow diagram is
shown in Fig 2.5.
(ii) We can see that the
domain ={1, 2, 3, 4, 5,}
Similarly, the range = {2, 3, 4, 5, 6}
and the codomain = {1, 2, 3, 4, 5, 6}
The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B. If n(A ) = p and n(B) = q, then n (A × B) = pq and the total number of relations is 2pq.
Example Let A = {1, 2} and B = {3, 4}. Find the number of relations from A to B.
Solution We have,
A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.
Since n (A×B ) = 4, the number of subsets of A×B is 24
. Therefore, the number of
relations from A into B will be 24
Remark A relation R from A to A is also stated as a relation on A
