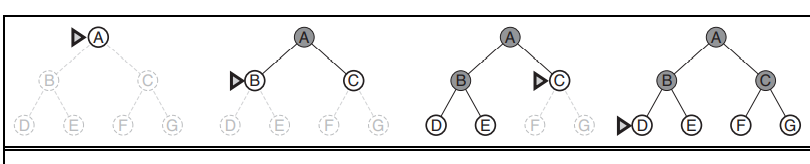
Breadth-first search is a simple strategy in which the root node is expanded first, then all the successors of the root node are expanded next, then their successors, and so on. In general, all the nodes are expanded at a given depth in the search tree before any nodes at the next level are expanded
Breadth-first search is an instance of the general graph-search algorithm in which the shallowest unexpanded node is chosen for expansion. This is achieved very simply by using a FIFO queue for the frontier. Thus, new nodes (which are always deeper than their parents) go to the back of the queue, and old nodes, which are shallower than the new nodes, get expanded first. There is one slight tweak on the general graph-search algorithm, which is that the goal test is applied to each node when it is generated rather than when it is selected for expansion
Breadth-first search on a graph
function BREADTH-FIRST-SEARCH(problem) returns a solution, or failure
node ←a node with STATE = problem.INITIAL-STATE, PATH-COST = 0
if problem.GOAL-TEST(node.STATE) then return SOLUTION(node)
frontier ← a FIFO queue with node as the only element
explored ← an empty set
loop do
if EMPTY?(frontier ) then return failure
node ← POP(frontier ) /* chooses the shallowest node in frontier */
add node.STATE to explored
for each action in problem.ACTIONS(node.STATE) do
child ← CHILD-NODE(problem, node, action)
if child.STATE is not in explored or frontier then
if problem.GOAL-TEST(child.STATE) then return SOLUTION(child)
frontier ← INSERT(child,frontier )
the total number of nodes generated is
b2 + b3 + ··· + bd = O(bd)
As for space complexity: for any kind of graph search, which stores every expanded node in the explored set, the space complexity is always within a factor of b of the time complexity. For breadth-first graph search in particular, every node generated remains in memory. There will be O(bd−1) nodes in the explored set and O(bd) nodes in the frontier so the space complexity is O(bd), i.e., it is dominated by the size of the frontier. Switching to a tree search would not save much space, and in a state space with many redundant paths, switching could cost a great deal of time
