uniform-cost search expands the node n with the lowest path cost g(n). This is done by storing the frontier as a priority queue ordered by g
Uniform-cost search on a graph
function UNIFORM-COST-SEARCH(problem) returns a solution, or failure
node ←a node with STATE = problem.INITIAL-STATE, PATH-COST = 0
frontier ← a priority queue ordered by PATH-COST, with node as the only element
explored ← an empty set
loop do
if EMPTY?(frontier ) then return failure
node ← POP(frontier ) /* chooses the lowest-cost node in frontier */
if problem.GOAL-TEST(node.STATE) then return SOLUTION(node)
add node.STATE to explored
for each action in problem.ACTIONS(node.STATE) do
child ← CHILD-NODE(problem, node, action)
if child.STATE is not in explored or frontier then
frontier ← INSERT(child,frontier )
else if child.STATE is in frontier with higher PATH-COST then
replace that frontier node with child
In addition to the ordering of the queue by path cost, there are two other significant differences from breadth-first search. The first is that the goal test is applied to a node when it is selected for expansion rather than when it is first generated. The reason is that the first goal node that is generated may be on a suboptimal path. The second difference is that a test is added in case a better path is found to a node currently on the frontier
It is easy to see that uniform-cost search is optimal in general. First, we observe that whenever uniform-cost search selects a node n for expansion, the optimal path to that node has been found
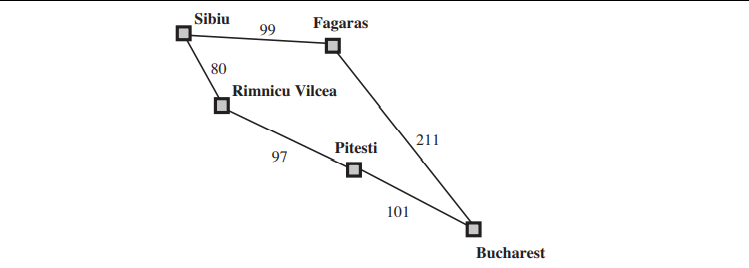
Uniform-cost search is guided by path costs rather than depths, so its complexity is not easily characterized in terms of b and d
