A free tree is a connected, acyclic, undirected graph. We often omit the adjective “free” when we say that a graph is a tree. If an undirected graph is acyclic but possibly disconnected, it is a forest. Many algorithms that work for trees also work for trees also work for forests. Figure B.4(a) shows a free tree, and Figure B.4(b) shows a forest. The forest in Figure B.4(b) is not a tree because it is not connected. The graph in Figure B.4(c) is connected but neither a tree nor a forest, because it contains a cycle.
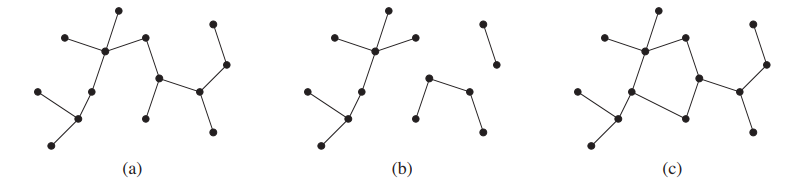
(a) A free tree. (b) A forest. (c) A graph that contains a cycle and is therefore neither a tree nor a forest.
Properties of free trees
- Let G D .V; E/ be an undirected graph. The following statements are equivalent
- is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected, and |E| D |V | – 1
- G is acyclic, and |E| D |V| – 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle
