A picture needs to be increased to twice it’s size or a picture is to be turned through 900. In all these cases, it is possible to view the new picture as really a new one and use algorithms to draw them, but a better method is, given their present form, try to get their new counter parts by operating on the existing data. This concept is called transformation
Matrix representation of points
Normally, we represent a point by two values in a rectangular coordinate systems as (x,y). x represents the distance of the point from the origin in the horizontal direction and y in the vertical directions. Negative values are intended to represent movement in the reverse direction (on a CRT screen, however, negative valued pixels can not be represented)
However, in the context of graphics we tend to represent a point as a 3 valued entity [ x y 1] where x and y are the coordinates and 1 is just added to the representation. But use of this additional value becomes significant shortly.
The basic Transformation
The three basic transformations are (i) Translation (ii) rotation and (iii) scaling. Translation refers to the shifting of a point to some other place, whose distance with regard to the present point is known. Rotation as the name suggests is to rotate a point about an axis. The axis can be any of the coordinates or simply any other specified line also. Scaling is the concept of increasing (or decreasing) the size of a picture. (in one or in either directions. When it is done in both directions, the increase or decrease in both directions need not be same) To change the size of the picture, we increase or decrease the distance between the end points of the picture and also change the intermediate points are per requirements;
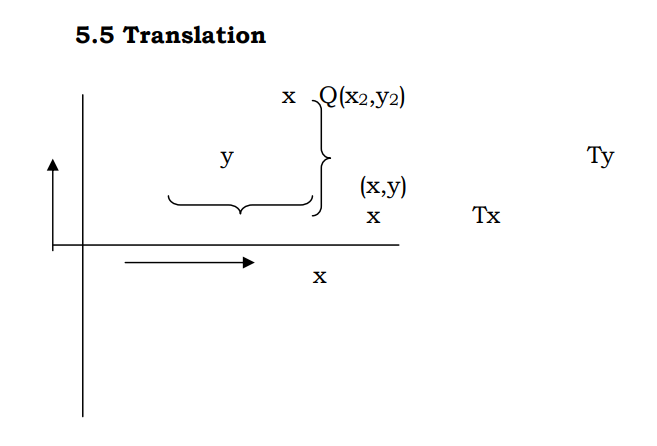
Consider a point P(x1, y1) to be translated to another point Q(x2, y2). If we know the point value (x2, y2) we can directly shift to Q by displaying the pixel (x2, y2). On the other hand, suppose we only know that we want to shift by a distance of Tx along x axis and Ty along Y axis. Then obviously the coordinates can be derived by x2 =x1 +Tx and Y2 = y1 + Ty.
Suppose we want to shift a triangle with coordinates at A(20,10), B(30,100 and C(40,70). The shifting to be done by 20 units along x axis and 10 units along y axis. Then the new triangle will be at A1 (20+20, 10+10) B1 (30+20, 10+10) C1 (40+20, 70+10)
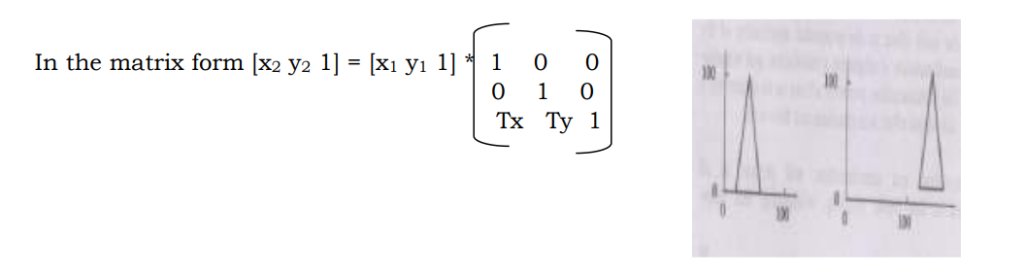
Rotation
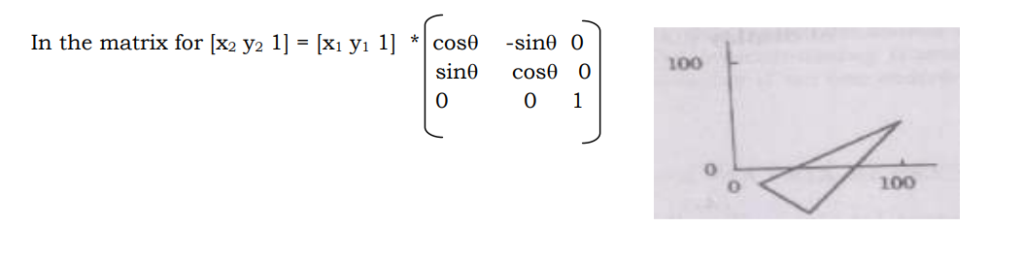
Suppose we want to rotate a point (x1 y1) clockwise through an angle⁄ about the origin of the coordinate system. Then mathematically we can show that
x2 = x1cosθ + y1sinθ and
y2 = x1sinθ – y1cosθ
These equations become applicable only if the rotation is about the origin.