Bresenham’s algorithm is designed on a very interesting feature of the DDA. At each stage, one of the coordinates changes by a value 1 (That is because we have made either (y2-y1) or x2-x1) equal to length, so that either (x2-x1)/length or (y2-y1)/length will be equal to 1). The other coordinate will either change by 1 or will remain constant. This is because, even though the value should change by a small value, because of the rounding off, the value may or may not be sufficient to take the point to the next level
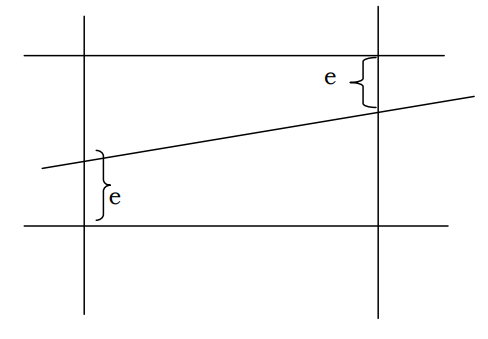
Look at the above figure. The left most point should have been at the point indicated by x, but because of rounding off, falls back to the previous pixel. Whereas in the second case, the point still falls below the next level, but because of the rounding off, goes to the next level. In each case, e is the error involved in the process.
So what the Bresenham algorithm does it as follows. In each case adds ∆y or ∆x as the case may be, to the previous value and finds the difference between the value and the (next) desirable point. This difference is the error e. If the error is >=1, then the point is incremented to the next level and 1 is subtracted from the value. If e is <1, we have not yet reached the point, where we should go to the next point, hence keep the display points unchanged
C Program to generate a line using Bresenham’s algorithm
# include<stdio.h>
# include<conio.h>
#include<stddlib.h>
# include <graphics.h>
void brline(int,int,int,int);
void main()
{
int gd=DETECT,gm,color:
int x1,y1,x2,y2;
printf(“\n enter the starting point x1,y1 :”);
scanf(“%d%d”,&x1,&y1);
printf(“\n enter the starting point x2,y2 :”);
scanf(“%d%d”,&x2,&y2);
clrscr();
initgraph(&gdriver, &gmode,””);
brline(x1,y1,x2,y2);
getch();
closegraph();
}
/* Function for Bresenham’s line */
void brline(int x1,int y1,int x2,int y2)
{
int e,l,xend;
int color;
float dx,dy,x,y;
dx=abs(x2-x1);
dy=abs(y2-y1);
if(x1>x2)
{
x=x2;
y=y2;
xend=x1;
}
else
{
x=x1;
y=y1;
xend=x2;
}
e=2*dy-dx;
while(x<xend)
{
color=random(getmaxcolor());
putpixel((int)x,(int)y,color);
if(e>0)
{
y++;
e=e+2*(dy-dx);
}
else
e=e+2*dy;
x++;
}
}
