A binary search tree, also known as an ordered binary tree, is a variant of binary trees in which the nodes are arranged in an order. In a binary search tree, all the nodes in the left sub-tree have a value less than that of the root node. Correspondingly, all the nodes in the right sub-tree have a value either equal to or greater than the root node. The same rule is applicable to every sub-tree in the tree.
Note that a binary search tree may or may not contain duplicate values, depending on its implementation
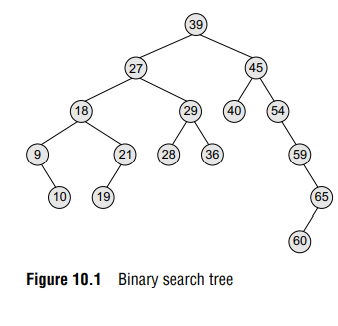
Look at Fig. 10.1. The root node is 39. The left sub-tree of the root node consists of nodes 9, 10, 18, 19, 21, 27, 28, 29, and 36. All these nodes have smaller values than the root node. The right sub-tree of the root node consists of nodes 40, 45, 54, 59, 60, and 65. Recursively, each of the sub-trees also obeys the binary search tree constraint. For example, in the left sub-tree of the root node, 27 is the root and all elements in its left sub-tree (9, 10, 18, 19, 21) are smaller than 27, while all nodes in its right sub-tree (28, 29, and 36) are greater than the root node’s value
Binary search trees also speed up the insertion and deletion operations. The tree has a speed advantage when the data in the structure changes rapidly
Binary search trees are considered to be efficient data structures especially when compared with sorted linear arrays and linked lists. In a sorted array, searching can be done in O(log2 n) time, but insertions and deletions are quite expensive. In contrast, inserting and deleting elements in a linked list is easier, but searching for an element is done in O(n) time.
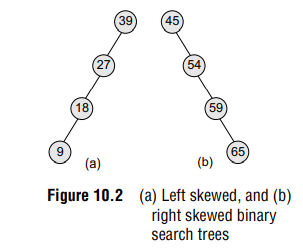
However, in the worst case, a binary search tree will take O(n) time to search for an element. The worst case would occur when the tree is a linear chain of nodes as given in Fig. 10.2.
Binary Search Trees properties
- The left sub-tree of a node N contains values that are less than N’s value
- The right sub-tree of a node N contains values that are greater than N’s value
- Both the left and the right binary trees also satisfy these properties and, thus, are binary search trees
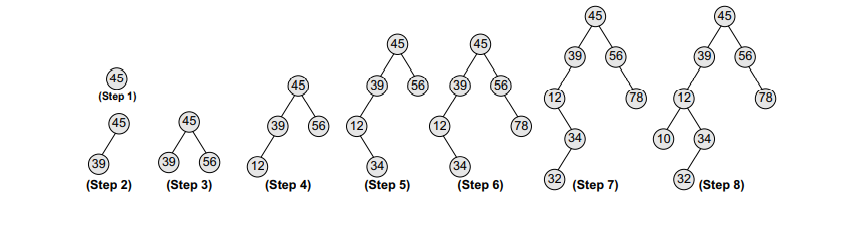
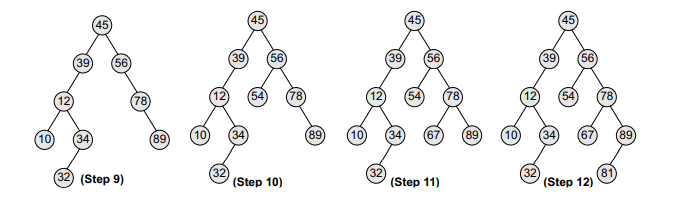
Example Create a binary search tree using the following data elements:
45, 39, 56, 12, 34, 78, 32, 10, 89, 54, 67, 81
Solution
Operations On Binary Search Trees
Searching for a Node in a Binary Search Tree
The search function is used to find whether a given value is present in the tree or not. The searching process begins at the root node. The function first checks if the binary search tree is empty. If it is empty, then the value we are searching for is not present in the tree. So, the search algorithm terminates by displaying an appropriate message. However, if there are nodes in the tree, then the search function checks to see if the key value of the current node is equal to the value to be searched. If not, it checks if the value to be searched for is less than the value of the current node, in which case it should be recursively called on the left child node. In case the value is greater than the value of the current node, it should be recursively called on the right child node
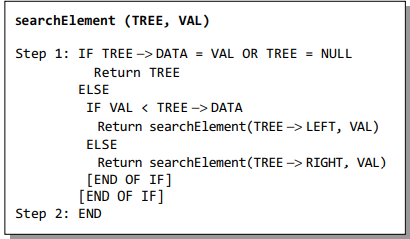
Inserting a New Node in a Binary Search Tree
The insert function is used to add a new node with a given value at the correct position in the binary search tree. Adding the node at the correct position means that the new node should not violate the properties of the binary search tree
The initial code for the insert function is similar to the search function. This is because we first find the correct position where the insertion has to be done and then add the node at that position. The insertion function changes the structure of the tree. Therefore, when the insert function is called recursively, the function should return the new tree pointer.

Deleting a Node from a Binary Search Tree
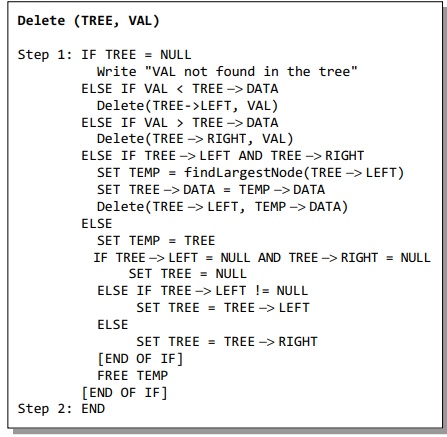
Determining the Height of a Binary Search Tree
In order to determine the height of a binary search tree, we calculate the height of the left sub-tree and the right sub-tree. Whichever height is greater, 1 is added to it. For example, if the height of the left sub-tree is greater than that of the right sub-tree, then 1 is added to the left sub-tree, else 1 is added to the right sub-tree.
Look at Fig. 10.16. Since the height of the right sub-tree is greater than the height of the left sub-tree, the height of the tree = height (right sub-tree) + 1= 2 + 1 = 3
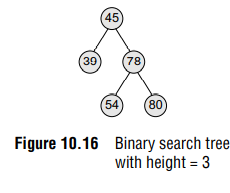
Determining the Number of Nodes
Determining the number of nodes in a binary search tree is similar to determining its height. To calculate the total number of elements/nodes in the tree, we count the number of nodes in the left sub-tree and the right sub-tree
Number of nodes = totalNodes(left sub–tree) + totalNodes(right sub–tree) + 1
Determining the Number of Internal Nodes
To calculate the total number of internal nodes or non-leaf nodes, we count the number of internal nodes in the left sub-tree and the right sub-tree and add 1 to it (1 is added for the root node)
number of internal nodes = totalInternalNodes(left sub–tree) + totalInternalNodes(right sub–tree) + 1
Determining the Number of External Nodes
Number of external nodes = totalExternalNodes(left sub–tree) + totalExternalNodes (right sub–tree)
Write a program to create a binary search tree and perform all the operations
#include <stdio.h>
#include <conio.h>
#include <malloc.h>
struct node
{
int data;
struct node *left;
struct node *right;
};
struct node *tree;
void create_tree(struct node *);
struct node *insertElement(struct node *, int);
void preorderTraversal(struct node *);
void inorderTraversal(struct node *);
void postorderTraversal(struct node *);
struct node *findSmallestElement(struct node *);
struct node *findLargestElement(struct node *);
struct node *deleteElement(struct node *, int);
struct node *mirrorImage(struct node *);
int totalNodes(struct node *);
int totalExternalNodes(struct node *);
int totalInternalNodes(struct node *);
int Height(struct node *);
struct node *deleteTree(struct node *);
int main()
{
int option, val;
struct node *ptr;
create_tree(tree);
clrscr();
do
{
printf("\n ******MAIN MENU******* \n");
printf("\n 1. Insert Element");
printf("\n 2. Preorder Traversal");
printf("\n 3. Inorder Traversal");
printf("\n 4. Postorder Traversal");
printf("\n 5. Find the smallest element");
printf("\n 6. Find the largest element");
printf("\n 7. Delete an element");
printf("\n 8. Count the total number of nodes");
printf("\n 9. Count the total number of external nodes");
printf("\n 10. Count the total number of internal nodes");
printf("\n 11. Determine the height of the tree");
printf("\n 12. Find the mirror image of the tree");
printf("\n 13. Delete the tree");
printf("\n 14. Exit");
printf("\n\n Enter your option : ");
scanf("%d", &option);
switch(option)
{
case 1:
printf("\n Enter the value of the new node : ");
scanf("%d", &val);
tree = insertElement(tree, val);
break;
case 2:
printf("\n The elements of the tree are : \n");
preorderTraversal(tree);
break;
case 3:
printf("\n The elements of the tree are : \n");
inorderTraversal(tree);
break;
case 4:
printf("\n The elements of the tree are : \n");
postorderTraversal(tree);
break;
case 5:
ptr = findSmallestElement(tree);
printf("\n Smallest element is :%d",ptr–>data);
break;
case 6:
ptr = findLargestElement(tree);
printf("\n Largest element is : %d", ptr–>data);
break;
case 7:
printf("\n Enter the element to be deleted : ");
scanf("%d", &val);
tree = deleteElement(tree, val);
break;
case 8:
printf("\n Total no. of nodes = %d", totalNodes(tree));
break;
case 9:
printf("\n Total no. of external nodes = %d",
totalExternalNodes(tree));
break;
case 10:
printf("\n Total no. of internal nodes = %d",
totalInternalNodes(tree));
break;
case 11:
printf("\n The height of the tree = %d",Height(tree));
break;
case 12:
tree = mirrorImage(tree);
break;
case 13:
tree = deleteTree(tree);
break;
}
}while(option!=14);
getch();
return 0;
}
void create_tree(struct node *tree)
{
tree = NULL;
}
struct node *insertElement(struct node *tree, int val)
{
struct node *ptr, *nodeptr, *parentptr;
ptr = (struct node*)malloc(sizeof(struct node));
ptr–>data = val;
ptr–>left = NULL;
ptr–>right = NULL;
if(tree==NULL)
{
tree=ptr;
tree–>left=NULL;
tree–>right=NULL;
}
else
{
parentptr=NULL;
nodeptr=tree;
while(nodeptr!=NULL)
{
parentptr=nodeptr;
if(val<nodeptr–>data)
nodeptr=nodeptr–>left;
else
nodeptr = nodeptr–>right;
}
if(val<parentptr–>data)
parentptr–>left = ptr;
else
parentptr–>right = ptr;
}
return tree;
}
void preorderTraversal(struct node *tree)
{
if(tree != NULL)
{
printf("%d\t", tree–>data);
preorderTraversal(tree–>left);
preorderTraversal(tree–>right);
}
}
void inorderTraversal(struct node *tree)
{
if(tree != NULL)
{
inorderTraversal(tree->left);
printf("%d\t", tree->data);
inorderTraversal(tree->right);
}
}
void postorderTraversal(struct node *tree)
{
if(tree != NULL)
{
postorderTraversal(tree->left);
postorderTraversal(tree->right);
printf("%d\t", tree->data);
}
}
struct node *findSmallestElement(struct node *tree)
{
if( (tree == NULL) || (tree->left == NULL))
return tree;
else
return findSmallestElement(tree ->left);
}
struct node *findLargestElement(struct node *tree)
{
if( (tree == NULL) || (tree->right == NULL))
return tree;
else
return findLargestElement(tree->right);
}
struct node *deleteElement(struct node *tree, int val)
{
struct node *cur, *parent, *suc, *psuc, *ptr;
if(tree–>left==NULL)
{
printf("\n The tree is empty ");
return(tree);
}
parent = tree;
cur = tree–>left;
while(cur!=NULL && val!= cur–>data)
{
parent = cur;
cur = (val<cur–>data)? cur–>left:cur–>right;
}
if(cur == NULL)
{
printf("\n The value to be deleted is not present in the tree");
return(tree);
}
if(cur–>left == NULL)
ptr = cur–>right;
else if(cur–>right == NULL)
ptr = cur–>left;
else
{
// Find the in–order successor and its parent
psuc = cur;
cur = cur–>left;
while(suc–>left!=NULL)
{
psuc = suc;
suc = suc–>left;
}
if(cur==psuc)
{
// Situation 1
suc–>left = cur–>right;
}
else
{
// Situation 2
suc–>left = cur–>left;
psuc–>left = suc–>right;
suc–>right = cur–>right;
}
ptr = suc;
}
// Attach ptr to the parent node
if(parent–>left == cur)
parent–>left=ptr;
else
parent–>right=ptr;
free(cur);
return tree;
}
int totalNodes(struct node *tree)
{
if(tree==NULL)
return 0;
else
return(totalNodes(tree–>left) + totalNodes(tree–>right) + 1);
}
int totalExternalNodes(struct node *tree)
{
if(tree==NULL)
return 0;
else if((tree–>left==NULL) && (tree–>right==NULL))
return 1;
else
return (totalExternalNodes(tree–>left) +
totalExternalNodes(tree–>right));
}
int totalInternalNodes(struct node *tree)
{
if( (tree==NULL) || ((tree–>left==NULL) && (tree–>right==NULL)))
return 0;
else
return (totalInternalNodes(tree–>left)
+ totalInternalNodes(tree–>right) + 1);
}
int Height(struct node *tree)
{
int leftheight, rightheight;
if(tree==NULL)
return 0;
else
{
leftheight = Height(tree–>left);
rightheight = Height(tree–>right);
if(leftheight > rightheight)
return (leftheight + 1);
else
return (rightheight + 1);
}
}
struct node *mirrorImage(struct node *tree)
{
struct node *ptr;
if(tree!=NULL)
{
mirrorImage(tree–>left);
mirrorImage(tree–>right);
ptr=tree–>left;
ptr–>left = ptr–>right;
tree–>right = ptr;
}
}
struct node *deleteTree(struct node *tree)
{
if(tree!=NULL)
{
deleteTree(tree–>left);
deleteTree(tree–>right);
free(tree);
}
}
Output
*******MAIN MENU*******
1. Insert Element
2. Preorder Traversal
3. Inorder Traversal
4. Postorder Traversal
5. Find the smallest element
6. Find the largest element
7. Delete an element
8. Count the total number of nodes
9. Count the total number of external nodes
10. Count the total number of internal nodes
11. Determine the height of the tree
12. Find the mirror image of the tree
13. Delete the tree
14. Exit
Enter your option : 1
Enter the value of the new node : 1
Enter the value of the new node : 2
Enter the value of the new node : 4
Enter your option : 3
2 1 4
Enter your option : 14
