Arithmetic code for two-symbol sequences
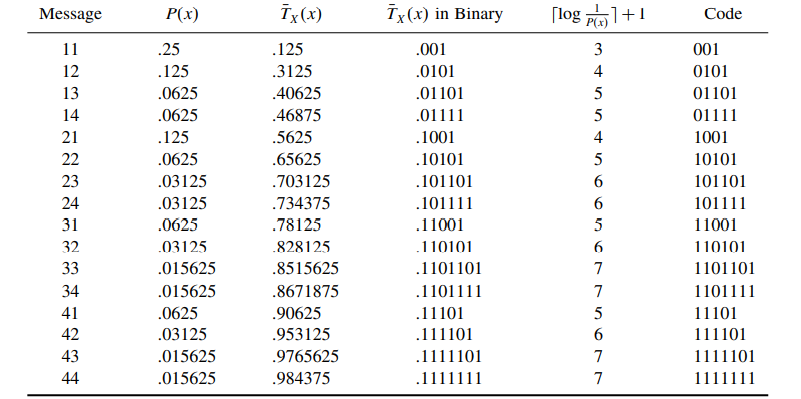
The average length per message is 4.5 bits. Therefore, using two symbols at a time we get a rate of 2.25 bits/symbol (certainly better than 2.75 bits/symbol, but still not as good as the best rate of 1.75 bits/symbol). However, we see that as we increase the number of symbols per message, our results get better and better
Recall that the bounds on the average length lA of the arithmetic code are
H(X) ≤ lA ≤ H(X)+ 2 /m
It does not take many symbols in a sequence before the coding rate for the arithmetic code becomes quite close to the entropy. However, recall that for Huffman codes, if we block m symbols together, the coding rate is
H(X) ≤ lH ≤ H(X)+ 1/m
The advantage seems to lie with the Huffman code, although the advantage decreases with increasing m. However, remember that to generate a codeword for a sequence of length m, using the Huffman procedure requires building the entire code for all possible sequences of length m. If the original alphabet size was k, then the size of the codebook would be km. Taking relatively reasonable values of k = 16 and m = 20 gives a codebook size of 1620! This is obviously not a viable option. For the arithmetic coding procedure, we do not need to build the entire codebook. Instead, we simply obtain the code for the tag corresponding to a given sequence. Therefore, it is entirely feasible to code sequences of length 20 or much more. In practice, we can make m large for the arithmetic coder and not for the Huffman coder. This means that for most sources we can get rates closer to the entropy using arithmetic coding than by using Huffman coding. The exceptions are sources whose probabilities are powers of two. In these cases, the single-letter Huffman code achieves the entropy, and we cannot do any better with arithmetic coding, no matter how long a sequence we pick
