Most of the relationships between sets can be represented by means of diagrams which are known as Venn diagrams. Venn diagrams are named after the English logician, John Venn (1834-1883). These diagrams consist of rectangles and closed curves usually circles. The universal set is represented usually by a rectangle and its subsets by circles
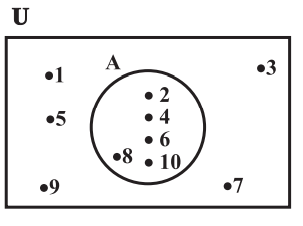
Example of Venn diagrams
U = {1,2,3, …, 10} is the universal set of which A = {2,4,6,8,10} is a subset
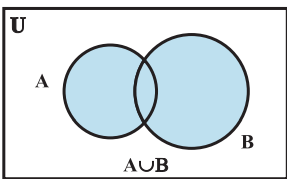
Venn Diagrams of Union of sets
Let A and B be any two sets. The union of A and B is the set which consists of all the elements of A and all the elements of B, the common elements being taken only once. The symbol ‘∪’ is used to denote the union. Symbolically, we write A ∪ B and usually read as ‘A union B’
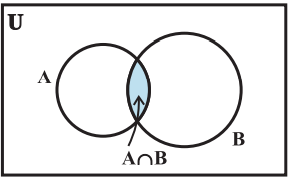
Venn diagrams of Intersection of sets
The intersection of sets A and B is the set of all elements which are common to both A and B. The symbol ‘∩’ is used to denote the intersection. The intersection of two sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write A ∩ B = {x : x ∈ A and x ∈ B}