To understand Statistical learning models in Artificial intelligence
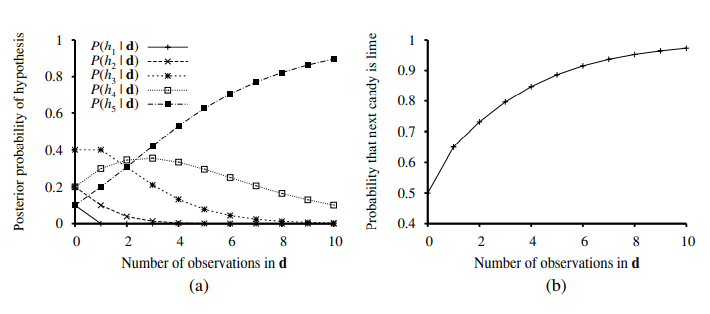
Consider a simple example. Our favorite Surprise candy comes in two flavors: cherry (yum) and lime (ugh). The manufacturer has a peculiar sense of humor and wraps each piece of candy in the same opaque wrapper, regardless of flavor. The candy is sold in very large bags, of which there are known to be five kinds—again, indistinguishable from the outside:
h1: 100% cherry,
h2: 75% cherry + 25% lime,
h3: 50% cherry + 50% lime,
h4: 25% cherry + 75% lime,
h5: 100% lime
Given a new bag of candy, the random variable H (for hypothesis) denotes the type of the bag, with possible values h1 through h5. H is not directly observable, of course. As the pieces of candy are opened and inspected, data are revealed—D1, D2, …, DN , where each Di is a random variable with possible values cherry and lime. The basic task faced by the agent is to predict the flavor of the next piece of candy.1 Despite its apparent triviality, this scenario serves to introduce many of the major issues. The agent really does need to infer a theory of its world, albeit a very simple one
Bayesian learning simply calculates the probability of each hypothesis, given the data, and makes predictions on that basis. That is, the predictions are made by using all the hypotheses, weighted by their probabilities, rather than by using just a single “best” hypothesis. In this way, learning is reduced to probabilistic inference. Let D represent all the data, with observed value d; then the probability of each hypothesis is obtained by Bayes’ rule:
P(hi | d) = αP(d | hi)P(hi)