Asymptotic Notations

Asymptotic analysis is a measure of efficiency of algorithms that doesn’t depend on machine specific constants, and doesn’t require algorithms to be implemented and time taken by programs to be compared. Asymptotic notations are mathematical tools to represent time complexity of algorithms for asymptotic analysis. The following three asymptotic notations are mostly used to represent time complexity of algorithms

The Big O Notation:

The Big O notation defines an upper bound of an algorithm, it bounds a function only from above. For example, consider the case of Insertion Sort. It takes linear time in best case and quadratic time in worst case. We can safely say that the time complexity of Insertion sort is O(n2 ). Note that O(n2 ) also covers linear time

The Big O notation is useful when we only have upper bound on time complexity of an algorithm. Many times we easily find an upper bound by simply looking at the algorithm

For a given function g(n), we denote by O(g(n)) the set of functions

O(g(n)) = { f(n): there exist positive constants c and n0, such that 0 ≤ f(n)≤ c×g(n) for all n ≥ n0}

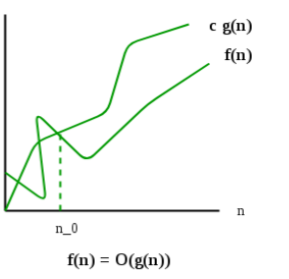
Example of Big O Notation

f(n) = 2n + 3
2n + 3 ≤ 10 n ∀ n ≥ 1
Here, c=10, n0=1, g(n)=n
=> f(n) = O(n)
Also, 2n + 3 ≤ 2 n + 3n
2n + 3 ≤ 5 n ∀ n ≥ 1
And, 2n + 3 ≤ 2n² + 3n²
2n + 3 ≤ 5n²
=> f(n) = O(n²)

O(1) < O(log n) < O(√ n) < O(n) < O(n log n) < O(n² ) < O(n3 ) < O(2ⁿ ) < O(3ⁿ ) < O(nⁿ)

The Omega (Ω) notation:

Just as Big O notation provides an asymptotic upper bound on a function, Ω notation provides an asymptotic lower bound.

Ω notation can be useful when we have lower bound on time complexity of an algorithm. As discussed in the previously, the best case performance of an algorithm is generally not useful, the omega notation is the least used notation among all three

For a given function g(n), we denote by Ω(g(n)) the set of functions.

Ω (g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ c×g(n) ≤ f(n) for all n ≥ n0 }.

Let us consider the same insertion sort example here. The time complexity of insertion sort can be written as Ω(n), but it is not a very useful information about insertion sort, as we are generally interested in worst case and sometimes in average case.

Example of The Omega (Ω) notation

f(n) = 2n + 3
2n + 3 ≥ n ∀ n ≥ 1
Here, c=1, n0=1, g(n)=n
=> f(n) = Ω(n)
Also, f(n) = Ω(log n)
f(n) = Ω(√n)

The Theta (Θ) notation:

The theta notation bounds a functions from above and below, so it defines the exact asymptotic behaviour. A simple way to get theta notation of an expression is to drop low order terms and ignore leading constants. For example, consider the following expression

3n³ + 6n² + 6000 = Θ(n³)

Dropping lower order terms is always fine because there will always be a n₀ after which Θ(n³ ) has higher values than Θ(n³ ) irrespective of the constants involved. For a given function g(n), we denote Θ(g(n)) as the following set of functions

Θ(g(n)) = {f(n): there exist positive constants c₁, c₂ and n₀ such that 0 ≤ c₁×g(n) ≤ f(n) ≤ c₂×g(n) for all n ≥ n₀}

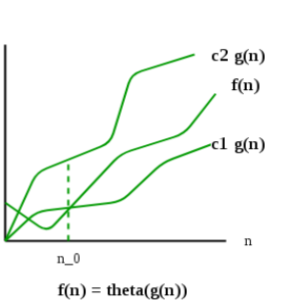
The above definition means, if f(n) is theta of g(n), then the value f(n) is always between c1×g(n) and c2×g(n) for large values of n (n ≥ n0). The definition of theta also requires that f(n) must be non-negative for values of n greater than n₀

Example of The Theta (Θ) notation:

Example:1

f(n) = 2n + 3
1 * n ≤ 2n + 3 ≤ 5n ∀ n ≥ 1
Here, c1=1, c2 = 5, n0=1, g(n)=n
=> f(n) = Θ(n)

Example:2

f(n) = 2n2 + 3n + 4
2n² + 3n + 4 ≤ 2n² + 3n² + 4n²
2n² + 3n + 4 ≤ 9n²
f(n) = O (n²)
also, 2n² + 3n + 4 ≥ 1 * n²
f(n) = Ω (n²)
=>1 * n² ≤ 2n² + 3n + 4 ≤ 9n² ∀ n ≥ 1
Here, c1=1, c2 = 9, n0=1, g(n)= n²
=> f(n) = Θ(n²)

Example:2

f(n) = n!
= 1 × 2 × 3 × 4 × … × n
1 × 1 × 1 × … × 1 ≤ 1 × 2 × 3 × 4 × … × n ≤ n × n × n × … × n
1 ≤ n! ≤ nⁿ
Ω (1) O (nⁿ)