The simplest approach to restoration is direct inverse filtering where we complete anestimate of the transform of the original image simply by dividing the transform of the degraded image G(u,v) by degradation
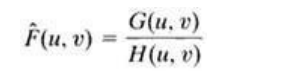
function H(u,v)
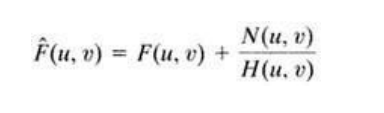
We know that
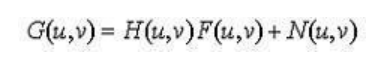
Therefore
From the above equation we observe that we cannot recover the undegraded image exactly because N(u,v) is a random function whose Fourier transform is not known. One approach to get around the zero or small-value problem is to limit the filter frequencies to values near the origin.We know that H(0,0) is equal to the average values of h(x,y). By Limiting the analysis to frequencies near the origin we reduse the probability of encountering zero values
