An image can be smoothed by attenuating the high-frequency components of its Fourier transform. Because edges and other abrupt changes in intensities are associated with high-frequency components, image sharpening can be achieved in the frequency domain by high pass filtering, which attenuates the low-frequency components without disturbing high frequency information in the Fourier transform.
The filter function H(u,v) are understood to be discrete functions of size PxQ; that is the discrete frequency variables are in the range
u = 0,1, 2…….,P-1 and
v = 0,1,2,…….,(Q-1)
The meaning of sharpening is edges and fine detail characterized by sharp transitions in image intensity. Such transitions contribute significantly to high frequency components of Fourier transform. Intuitively, attenuating certain low frequency components and preserving high frequency components result in sharpening. Intended goal is to do the reverse operation of low-pass filters.
When low-pass filter attenuated frequencies, high-pass filter passes them.
When high-pass filter attenuates frequencies, low-pass filter passes them. A high pass filter is obtained from a given low pass filter using the equation.
Hhp (u,v) = 1- Htp (u,v)
Where Hlp (u,v) is the transfer function of the low-pass filter. That is when the low- pass filter attenuates frequencies, the high-pass filter passed them, and vice-versa.
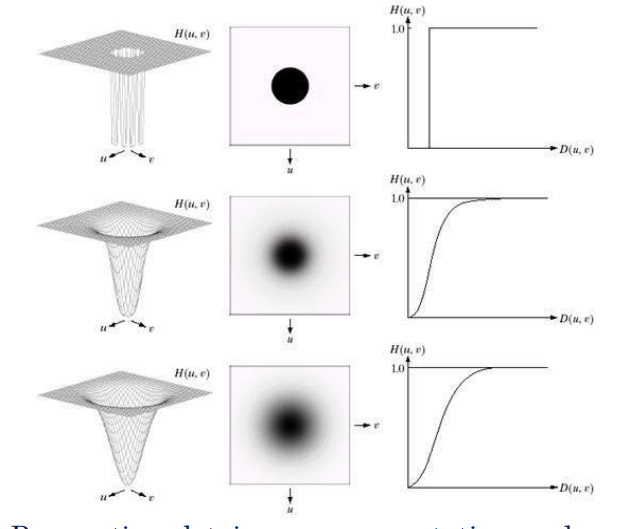
IDEAL HIGH-PASS FILTER:
A 2-D ideal high-pass filter (IHPF) is defined as
H (u,v) = 0, if D(u,v) ≤ D0
H (u,v) = 1, if D(u,v) ˃ D0
Where D0 is the cutoff frequency and D(u,v) is given by eq. As intended, the IHPF is the opposite of the ILPF in the sense that it sets to zero all frequencies inside a circle of radius D0 while passing, without attenuation, all frequencies outside the circle. As in case of the ILPF, the IHPF is not physically realizable
