Almost all reinforcement learning algorithms involve estimating value functions—functions of states (or of state–action pairs) that estimate how good it is for the agent to be in a given state (or how good it is to perform a given action in a given state). The notion of “how good” here is defined in terms of future rewards that can be expected, or, to be precise, in terms of expected return. Of course the rewards the agent can expect to receive in the future depend on what actions it will take. Accordingly, value functions are defined with respect to particular policies.
Recall that a policy, π, is a mapping from each state, s ∈ S, and action, a ∈ A(s), to the probability π(a|s) of taking action a when in state s. Informally, the value of a state s under a policy π, denoted vπ(s), is the expected return when starting in s and following π thereafter. For MDPs, we can define vπ(s) formally as
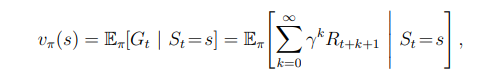
where Eπ[·] denotes the expected value of a random variable given that the agent follows policy π, and t is any time step. Note that the value of the terminal state, if any, is always zero. We call the function vπ the state-value function for policy π.
