Action-Value Methods in Artificial intelligence
True value of an action is the mean reward received when that action is selected. One natural way to estimate this is by averaging the rewards actually received when the action was selected. In other words, if by the tth time step action a has been chosen Nt(a) times prior to t, yielding rewards R1, R2, . . . , RNt(a) , then its value is estimated to be
The simplest action selection rule is to select the action (or one of the actions) with highest estimated action value, that is, to select at step t one of the greedy actions, A*t , for which Qt(A∗ t ) = maxa Qt(a). This greedy action selection method can be written as
At = argmax a Qt(a),
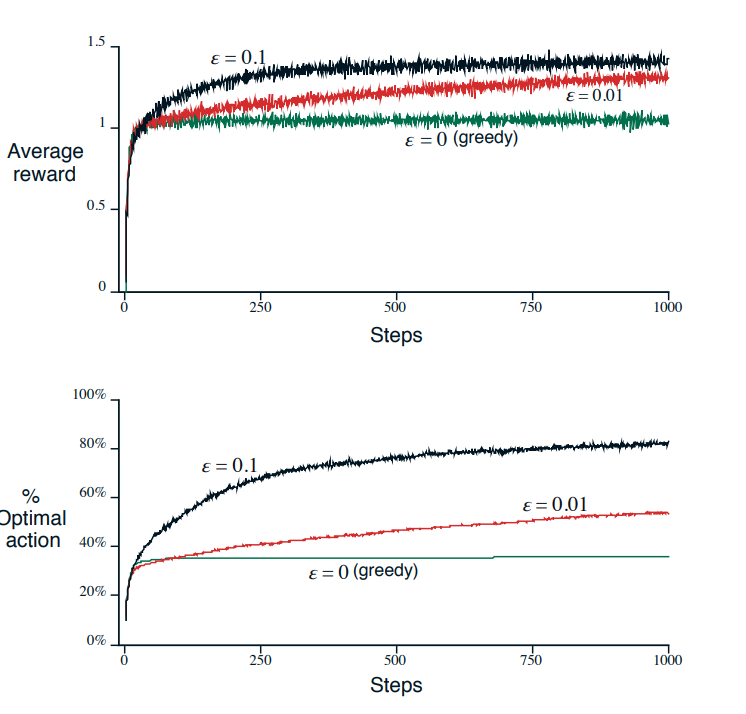
where argmaxa denotes the value of a at which the expression that follows is maximized (with ties broken arbitrarily). Greedy action selection always exploits current knowledge to maximize immediate reward; it spends no time at all sampling apparently inferior actions to see if they might really be better. A simple alternative is to behave greedily most of the time, but every once in a while, say with small probability ε, instead to select randomly from amongst all the actions with equal probability independently of the action value estimates.
We call methods using this near-greedy action selection rule ε-greedy methods. An advantage of these methods is that, in the limit as the number of plays increases, every action will be sampled an infinite number of times, guaranteeing that Nt(a) → ∞ for all a, and thus ensuring that all the Qt(a) converge to q(a). This of course implies that the probability of selecting the optimal action converges to greater than 1 − ε, that is, to near certainty. These are just asymptotic guarantees, however, and say little about the practical effectiveness of the methods