The algorithm for in-order traversal of a threaded binary tree
- Check if the current node has a left child that has not been visited. If a left child exists that has not been visited, go to Step 2, else go to Step 3.
- Add the left child in the list of visited nodes. Make it as the current node and then go to Step 6.
- If the current node has a right child, go to Step 4 else go to Step 5.
- Make that right child as current node and go to Step 6.
- Print the node and if there is a threaded node make it the current node.
- If all the nodes have visited then END else go to Step 1.
Let’s consider the threaded binary tree
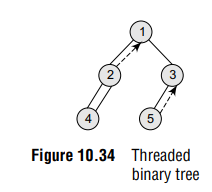
- Node 1 has a left child i.e., 2 which has not been visited. So, add 2 in the list of visited nodes, make it as the current node.
- Node 2 has a left child i.e., 4 which has not been visited. So, add 4 in the list of visited nodes, make it as the current node
- Node 4 does not have any left or right child, so print 4 and check for its threaded link. It has a threaded link to node 2, so make node 2 the current node
- Node 2 has a left child which has already been visited. However, it does not have a right child. Now, print 2 and follow its threaded link to node 1. Make node 1 the current node.
- Node 1 has a left child that has been already visited. So print 1. Node 1 has a right child 3 which has not yet been visited, so make it the current node.
- Node 3 has a left child (node 5) which has not been visited, so make it the current node.
- Node 5 does not have any left or right child. So print 5. However, it does have a threaded link which points to node 3. Make node 3 the current node
- Node 3 has a left child which has already been visited. So print 3.
- Now there are no nodes left, so we end here. The sequence of nodes printed is—4 2 1 5 3
Advantages of Threaded Binary Tree
- It enables linear traversal of elements in the tree.
- Linear traversal eliminates the use of stacks which in turn consume a lot of memory space and computer time.
- It enables to find the parent of a given element without explicit use of parent pointers.
- Since nodes contain pointers to in-order predecessor and successor, the threaded tree enables forward and backward traversal of the nodes as given by in-order fashion.
Thus, we see the basic difference between a binary tree and a threaded binary tree is that in binary trees a node stores a NULL pointer if it has no child and so there is no way to traverse back.
program to implement simple right in-threaded binary trees.
#include <stdio.h>
#include <conio.h>
struct tree
{
int val;
struct tree *right;
struct tree *left;
int thread;
};
struct tree *root = NULL;
struct tree* insert_node(struct tree *root, struct tree *ptr, struct tree *rt)
{
if(root == NULL)
{
root = ptr;
if(rt != NULL)
{
root–>right = rt;
root–>thread = 1;
}
}
else if(ptr–>val < root–>val)
root–>left = insert_node(root–>left, ptr, root);
else
if(root–>thread == 1)
{
root–>right = insert_node(NULL, ptr, rt);
root–>thread=0;
}
else
root–>right = insert_node(root–>right, ptr, rt);
return root;
}
struct tree* create_threaded_tree()
{
struct tree *ptr;
int num;
printf("\n Enter the elements, press –1 to terminate ");
scanf("%d", &num);
while(num != –1)
{
ptr = (struct tree*)malloc(sizeof(struct tree));
ptr–>val = num;
ptr–>left = ptr–>right = NULL;
ptr–>thread = 0;
root = insert_node(root, ptr, NULL);
printf(" \n Enter the next element ");
fflush(stdin);
scanf("%d", &num);
}
return root;
}
void inorder(struct tree *root)
{
struct tree *ptr = root, *prev;
do
{
while(ptr != NULL)
{
prev = ptr;
ptr = ptr–>left;
}
if(prev != NULL)
{
printf(" %d", prev–>val);
ptr = prev–>right;
while(prev != NULL && prev–>thread)
{
printf(" %d", ptr–>val);
prev = ptr;
ptr = ptr–>right;
}
}
}while(ptr != NULL);
}
void main()
{
// struct tree *root=NULL;
clrscr();
create_threaded_tree();
printf(" \n The in–order traversal of the tree can be given as : ");
inorder(root);
getch();
}
Output
Enter the elements, press –1 to terminate 5
Enter the next element 8
Enter the next element 2
Enter the next element 3
Enter the next element 7
Enter the next element –1
The in–order traversal of the tree can be given as:
2 3 5 7 8
