AVL tree is a self-balancing binary search tree invented by G.M. Adelson-Velsky and E.M. Landis in 1962. The tree is named AVL in honour of its inventors. In an AVL tree, the heights of the two sub-trees of a node may differ by at most one. Due to this property, the AVL tree is also known as a height-balanced tree. The key advantage of using an AVL tree is that it takes O(log n) time to perform search, insert, and delete operations in an average case as well as the worst case because the height of the tree is limited to O(log n).
BalanceFactor
The structure of an AVL tree is the same as that of a binary search tree but with a little difference. In its structure, it stores an additional variable called the BalanceFactor. Thus, every node has a balance factor associated with it. The balance factor of a node is calculated by subtracting the height of its right sub-tree from the height of its left sub-tree. A binary search tree in which every node has a balance factor of –1, 0, or 1 is said to be height balanced. A node with any other balance factor is considered to be unbalanced and requires rebalancing of the tree.
Balance factor = Height (left sub-tree) – Height (right sub-tree)
- If the balance factor of a node is 1, then it means that the left sub-tree of the tree is one level higher than that of the right sub-tree. Such a tree is therefore called as a left-heavy tree.
- If the balance factor of a node is 0, then it means that the height of the left sub-tree (longest path in the left sub-tree) is equal to the height of the right sub-tree.
- If the balance factor of a node is –1, then it means that the left sub-tree of the tree is one level lower than that of the right sub-tree. Such a tree is therefore called as a right-heavy tree
Look at Fig. 10.35. Note that the nodes 18, 39, 54, and 72 have no children, so their balance factor = 0. Node 27 has one left child and zero right child. So, the height of left sub-tree = 1, whereas the height of right sub-tree = 0. Thus, its balance factor = 1. Look at node 36, it has a left sub-tree with height = 2, whereas the height of right sub-tree = 1. Thus, its balance factor = 2 – 1 = 1. Similarly, the balance factor of node 45 = 3 – 2 =1; and node 63 has a balance factor of 0 (1 – 1).
Now, look at Figs 10.35 (a) and (b) which show a right-heavy AVL tree and a balanced AVL tree.
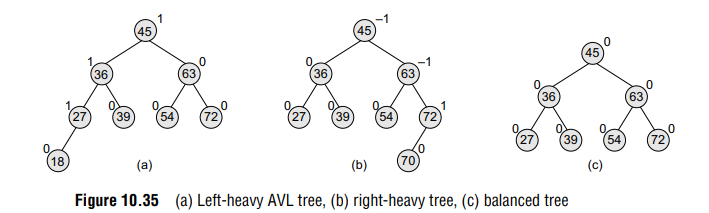
The trees given in Fig. 10.35 are typical candidates of AVL trees because the balancing factor of every node is either 1, 0, or –1. However, insertions and deletions from an AVL tree may disturb the balance factor of the nodes and, thus, rebalancing of the tree may have to be done. The tree is rebalanced by performing rotation at the critical node. There are four types of rotations: LL rotation, RR rotation, LR rotation, and RL rotation. The type of rotation that has to be done will vary depending on the particular situation. In the following section, we will discuss insertion, deletion, searching, and rotations in AVL trees.
Operations on AVL Trees
Searching for a Node in an AVL Tree
Searching in an AVL tree is performed exactly the same way as it is performed in a binary search tree. Due to the height-balancing of the tree, the search operation takes O(log n) time to complete. Since the operation does not modify the structure of the tree, no special provisions are required.
Inserting a New Node in an AVL Tree
Insertion in an AVL tree is also done in the same way as it is done in a binary search tree. In the AVL tree, the new node is always inserted as the leaf node. But the step of insertion is usually followed by an additional step of rotation. Rotation is done to restore the balance of the tree. However, if insertion of the new node does not disturb the balance factor, that is, if the balance factor of every node is still –1, 0, or 1, then rotations are not required.
During insertion, the new node is inserted as the leaf node, so it will always have a balance factor equal to zero. The only nodes whose balance factors will change are those which lie in the path between the root of the tree and the newly inserted node. The possible changes which may take place in any node on the path are as follows:
- Initially, the node was either left- or right-heavy and after insertion, it becomes balanced
- Initially, the node was balanced and after insertion, it becomes either left- or right-heavy.
- Initially, the node was heavy (either left or right) and the new node has been inserted in the heavy sub-tree, thereby creating an unbalanced sub-tree. Such a node is said to be a critical node
Consider the AVL tree given in Fig. 10.36.
If we insert a new node with the value 30, then the new tree will still be balanced and no rotations will be required in this case. Look at the tree given in Fig. 10.37 which shows the tree after inserting node 30.
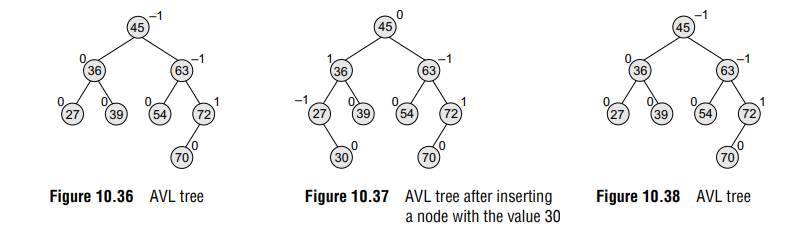
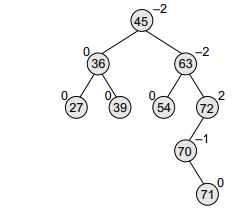
Let us take another example to see how insertion can disturb the balance factors of the nodes and how rotations are done to restore the AVL property of a tree. Look at the tree given in Fig. 10.38. After inserting a new node with the value 71, the new tree will be as shown in Fig. 10.39. Note that there are three nodes in the tree that have their balance factors 2, –2, and –2, thereby disturbing the AVLness of the tree. So, here comes the need to perform rotation.
To perform rotation, our first task is to find the critical node. Critical node is the nearest ancestor node on the path from the inserted node to the root whose balance factor is neither –1, 0, nor 1. In the tree given above, the critical node is 72. The second task in rebalancing the tree is to determine which type of rotation has to be done. There are four types of rebalancing rotations and application of these rotations depends on the position of the inserted node with reference to the critical node. The four categories of rotations are:
- LL rotation The new node is inserted in the left sub-tree of the left sub-tree of the critical node.
- RR rotation The new node is inserted in the right sub-tree of the right sub-tree of the critical node
- LR rotation The new node is inserted in the right sub-tree of the left sub-tree of the critical node.
- RL rotation The new node is inserted in the left sub-tree of the right sub-tree of the critical node.
LL Rotation
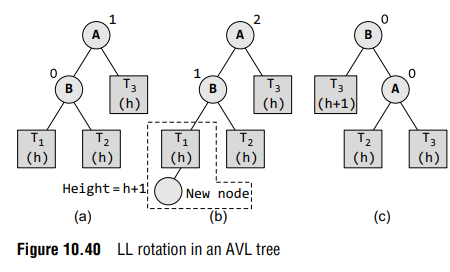
Let us study each of these rotations in detail. First, we will see where and how LL rotation is applied. Consider the tree given in Fig. 10.40 which shows an AVL tree.
Tree (a) is an AVL tree. In tree (b), a new node is inserted in the left sub-tree of the left sub-tree of the critical node A (node A is the critical node because it is the closest ancestor whose balance factor is not –1, 0, or 1), so we apply LL rotation as shown in tree (c).
While rotation, node B becomes the root, with T1 and A as its left and right child. T2 and T3 become the left and right sub-trees of A
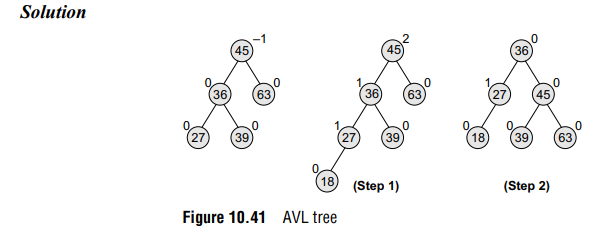
Example: Consider the AVL tree given in Fig. 10.41 and insert 18 into it.
Program that shows insertion operation in an AVL tree.
#include <stdio.h>
typedef enum { FALSE ,TRUE } bool;
struct node
{
int val;
int balance;
struct node *left_child;
struct node *right_child;
};
struct node* search(struct node *ptr, int data)
{
if(ptr!=NULL)
if(data < ptr -> val)
ptr = search(ptr -> left_child,data);
else if( data > ptr -> val)
ptr = search(ptr -> right_child, data);
return(ptr);
}
struct node *insert (int data, struct node *ptr, int *ht_inc)
{
struct node *aptr;
struct node *bptr;
if(ptr==NULL)
{
ptr = (struct node *) malloc(sizeof(struct node));
ptr -> val = data;
ptr -> left_child = NULL;
ptr -> right_child = NULL;
ptr -> balance = 0;
*ht_inc = TRUE;
return (ptr);
}
if(data < ptr -> val)
{
ptr -> left_child = insert(data, ptr -> left_child, ht_inc);
if(*ht_inc==TRUE)
{
switch(ptr -> balance)
{
case -1: /* Right heavy */
ptr -> balance = 0;
*ht_inc = FALSE;
break;
case 0: /* Balanced */
ptr -> balance = 1;
break;
case 1: /* Left heavy */
aptr = ptr -> left_child;
if(aptr -> balance == 1)
{
printf(“Left to Left Rotation\n”);
ptr -> left_child= aptr -> right_child;
aptr -> right_child = ptr;
ptr -> balance = 0;
aptr -> balance=0;
ptr = aptr;
}
else
{
printf(“Left to right rotation\n”);
bptr = aptr -> right_child;
aptr -> right_child = bptr -> left_child;
bptr -> left_child = aptr;
ptr -> left_child = bptr -> right_child;
bptr -> right_child = ptr;
if(bptr -> balance == 1 )
ptr -> balance = -1;
else
ptr -> balance = 0;
if(bptr -> balance == -1)
aptr -> balance = 1;
else
aptr -> balance = 0;
bptr -> balance=0;
ptr = bptr;
}
*ht_inc = FALSE;
}
}
}
if(data > ptr -> val)
{
ptr -> right_child = insert(info, ptr -> right_child, ht_inc);
if(*ht_inc==TRUE)
{
switch(ptr -> balance)
{
case 1: /* Left heavy */
ptr -> balance = 0;
*ht_inc = FALSE;
break;
case 0: /* Balanced */
ptr -> balance = -1;
break;
case -1: /* Right heavy */
aptr = ptr -> right_child;
if(aptr -> balance == -1)
{
printf(“Right to Right Rotation\n”);
ptr -> right_child= aptr -> left_child;
aptr -> left_child = ptr;
ptr -> balance = 0;
aptr -> balance=0;
ptr = aptr;
}
else
{
printf(“Right to Left Rotation\n”);
bptr = aptr -> left_child;
aptr -> left_child = bptr -> right_child;
bptr -> right_child = aptr;
ptr -> right_child = bptr -> left_child;
bptr -> left_child = pptr;
if(bptr -> balance == -1)
ptr -> balance = 1;
else
ptr -> balance = 0;
if(bptr -> balance == 1)
aptr -> balance = -1;
else
aptr -> balance = 0;
bptr -> balance=0;
ptr = bptr;
}/*End of else*/
*ht_inc = FALSE;
}
}
}
return(ptr);
}
void display(struct node *ptr, int level)
{
int i;
if ( ptr!=NULL )
{
display(ptr -> right_child, level+1);
printf(“\n”);
for (i = 0; i < level; i++)
printf(“ “);
printf(“%d”, ptr -> val);
display(ptr -> left_child, level+1);
}
}
void inorder(struct node *ptr)
{
if(ptr!=NULL)
{
inorder(ptr -> left_child);
printf(“%d “,ptr -> val);
inorder(ptr -> right_child);
}
}
main()
{
bool ht_inc;
int data ;
int option;
struct node *root = (struct node *)malloc(sizeof(struct node));
root = NULL;
while(1)
{
printf(“1.Insert\n”);
printf(“2.Display\n”);
printf(“3.Quit\n”);
printf(“Enter your option : “);
scanf(“%d”,&option);
switch(choice)
{
case 1:
printf(“Enter the value to be inserted : “);
scanf(“%d”, &data);
if( search(root,data) == NULL )
root = insert(data, root, &ht_inc);
else
printf(“Duplicate value ignored\n”);
break;
case 2:
if(root==NULL)
{
printf(“Tree is empty\n”);
continue;
}
printf(“Tree is :\n”);
display(root, 1);
printf(“\n\n”);
printf(“Inorder Traversal is: “);
inorder(root);
printf(“\n”);
break;
case 3:
exit(1);
default:
printf(“Wrong option\n”);
}
}
}
