Another property of coherence that can be made use of in scan conversion is the one-dimensional form of area coherence, called span coherence. If a pixel is inside a polygon, it’s neighbours also lie inside the polygon. This holds good upto a “Span” once the Span is detected, all pixels within the span can be set to the intensity value of the polygon and the next comparison can take place at the end of the span. This reduces the computation by a very large amount, especially if the no. of polygons is limited
The concept of spans can be considered in a simplistic manner by the following example.
In the 3-dimensional space, each scan line produces a plane. I.e. each scan line is for a particular value of y. A plane with this value of y as a constant over different values of x and z form a plane.
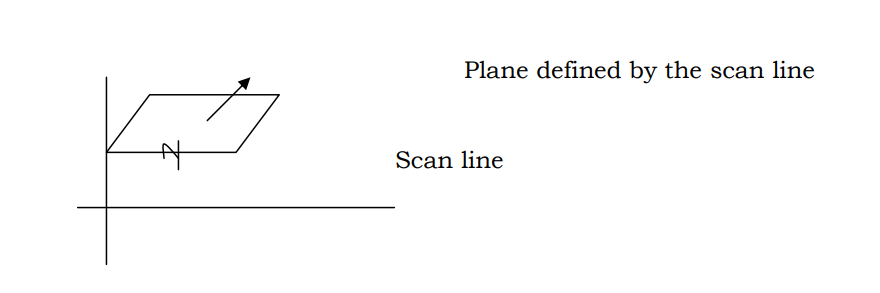
If one travels along this scan line, the plane intersects one/more polygons at different points. If these points of intersection are noted and are sorted in the increasing order of x, we get a sort of xz algorithm which gives the list of intersections with different polygons
Taking them in pairs, just as in the XY algorithm, one can convert the entire plane into several spans.
i. Spans that do not lie within any polygon, the pixels can be set to the background intensity
ii. Spans that lie within a single polygon. All of them can be set to the intensity of the polygon.
iii. Spans that are intersected by 2 or more polygons. In such spans, the pixel values can be set to the intensity of the nearest polygon.
