Every point needs to be checked as to whether it lies within the visible area of the pyramid by comparing the values of (D/S) xe and (D/s) ye to the end values of the visible area
i.e. -Ze ≤ (D/S) xe ≤ +Ze and -Ze ≤ (D/s) ye ≤ +Ze
This will exclude all points beyond the view point (ze ≤ 0) and all points that go beyond the visible pyramid
Note that this creates on problem. We indicated before that an object can be transformed to it’s perspective by simply mapping it’s endpoints. But, if these points go beyond the visible pyramid, then they cannot be displayed. But this does not mean the entire object cannot be rejected. The intersection of the visible pyramid with the profile of the object needs to be computed. This clipping has to work on a 3-dimensional perspective.
A three dimensional extending the 2-D scheme can derive clipping algorithm.
The algorithm determines whether the end point of the line lies in the visible pyramid by assigning a 4 bit code to it
First bit is 1: if the point is to the left the pyramid, else it will be zero, similarly,
Second bit : If the point is to the right of the pyramid
Third bit: If the point is below the pyramid
Fourth bit : If it is above the pyramid.
As earlier, if the codes for both the end points are 0000, then the line is trivially accepted. If the logical AND of the codes is not zero, both end points lie on the invisible side of one of the planes and can be trivially rejected. Otherwise the line crosses the side of the pyramid at one/more points. The point of intersection can be computed in the parametric form as
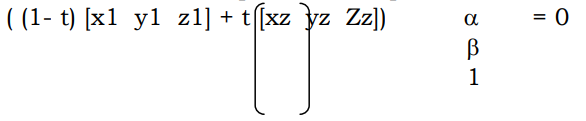
Where different values of α and β have different values for different planes. For example if α = 1 , β = 0, then it indicates the plane x=z. By substituting the various values of α and β one can find the point of intersection with different planes.
These Intersections then replace the ends of the line in the viewing pyramid.
Perspective view of a cube
We clarify the above discussions with an example, getting the perspective view of a cube. Consider a cube centered at the origin of the world coordinate system, defined by the following points and lines:
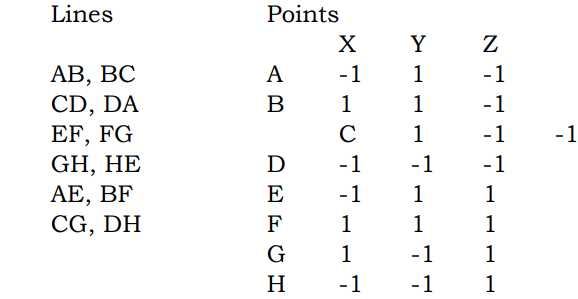
We shall observe this cube from a point (6, 8, 7.5) with the viewing axis ze pointed directly at the origin of the world coordinate system. There is still one degree of freedom left, namely an arbitrary rotation about the ze axis: we shall assume that the xe axis lies in the z = 7.5 plane.
The viewing transformation is established by a sequence of changes of coordinate systems. Recall that a transformation that moves a coordinate system is the inverse of the corresponding transformation that moves points
