Just as in the case of 2D, we represent the transformation operations as a series of matrix operations. With this, we obtain the flexibility of sequencing a series of operations one after the other to get the desired results on one hand and also the ability to undo the operations, by resorting to the reverse sequence. Since in the 2-dimensional case we were representing a point (x,y) as a tuple [x y 1], in the 3-dimensional case, we represent a point (x,y,z) as a [x y z 1]. The dimensions of the matrices grow from 3 x 3 to 4 x 4
Translations
Without repeating the earlier methods, we simply write
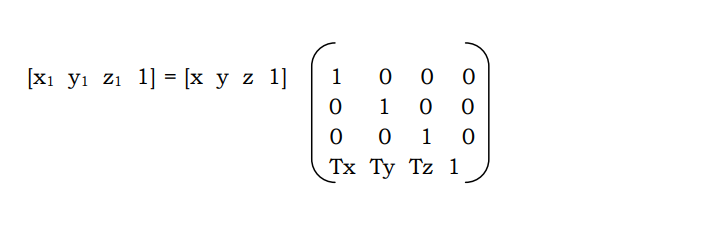
Where the point [ x y z 1 ] gets transformed to [ x1 y1 z1 1] after translating by Tx, Ty and Tz along the x,y,z directions respectively
