A perspective display can be generated by simply projecting every point of the object on to the plane of the screen. This section teaches you to get the coordinates (xs – ys) in the screen coordinates with respect to the eye coordinates (xe, ye, ze).
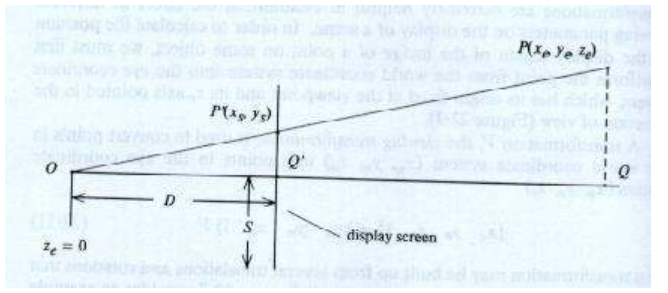
Consider the above figure, which indicates the basics of the perspective projection. O is the point behind the screen, which is called the “Perspective Point”, the point. The point P measured in eye coordinate is available at P(xe,ye,ze). The effort is to find the coordinates of the same point P(xs,ys) on the screen (also called screen coordinates) so that the perspective effect is established. D is the distance of the convergence point (where ze = 0) behind screen and S is half width of the screen.
The triangles OQ’P’ and OQP are similar.
Hence ys / D = ye / ze
Similarly it can be shown that
xs / D = xe /ze
The numbers xs and ys can be converted to fractions by dividing them by the screen size. This operation not only allows as to numbers which are fractions, but it also makes the numbers dimensionless (we are dividing a dimension with another dimension).
Xs / D = Xe /sze and Ys / D = Ye / S ze Or Xs = D xe / Sze and ys = D ye / Sze
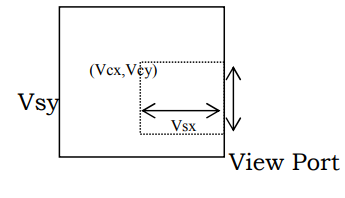
Alternatively they can be converted to the screen coordinates by including a specification of the location of view port in which the image is displayed.
Xs = (Dxe / Sze ) Vsx + Vcx and ys = (Dye /Sze ) Vsy + Vcy
The view port is at the centre (Vcx, Vcy) and is 2 Vsx units wide and 2 Vsy unit high