Rotation in 3-dimensions is a more complex affair. (In fact, even in 2 dimensions, rotation was more involved than scaling or translation because the concept of point of rotation). This is because; the rotation takes place about an axis. The same point, given the same amount of rotation, gets transformed to different points depending on which axis it was rotated
The simplest of the cases is to rotate the point about an axis that passes through the origin, and coincides with one of the axes x, y or z. The next complication arises when the axis passes through the origin, but does not coincide with any of the axes. The most general case would be, of course, when an arbitrary axis that does not pass through the origin becomes the axis of rotation.
Let us begin with simplest cases: The understanding is that a clockwise rotation, when viewed at the origin, standing on the axis is taken as positive and the other direction is negative. If this description looks too complicated, look at the following figures. In each case, we write down the transformation for the rotation through a positive angle of +θ
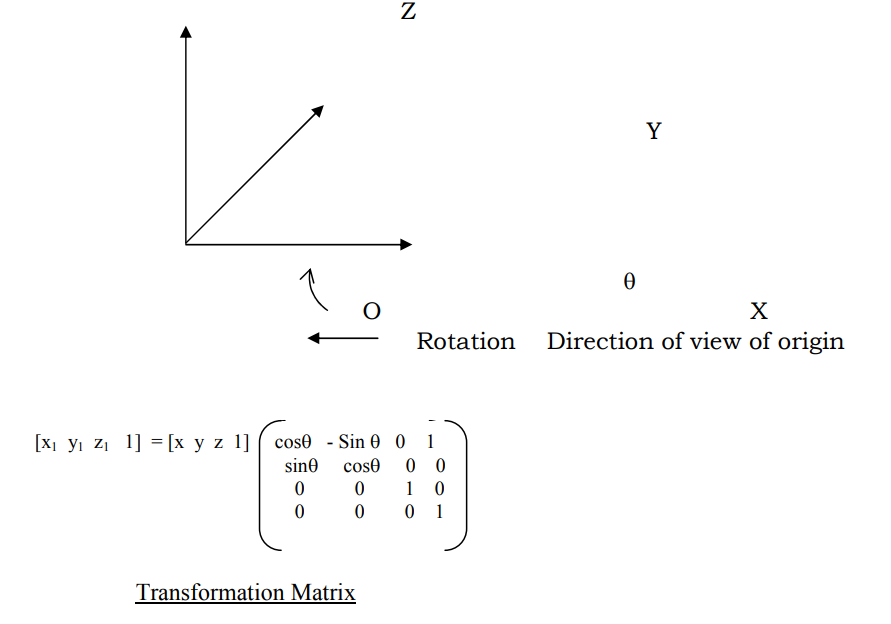
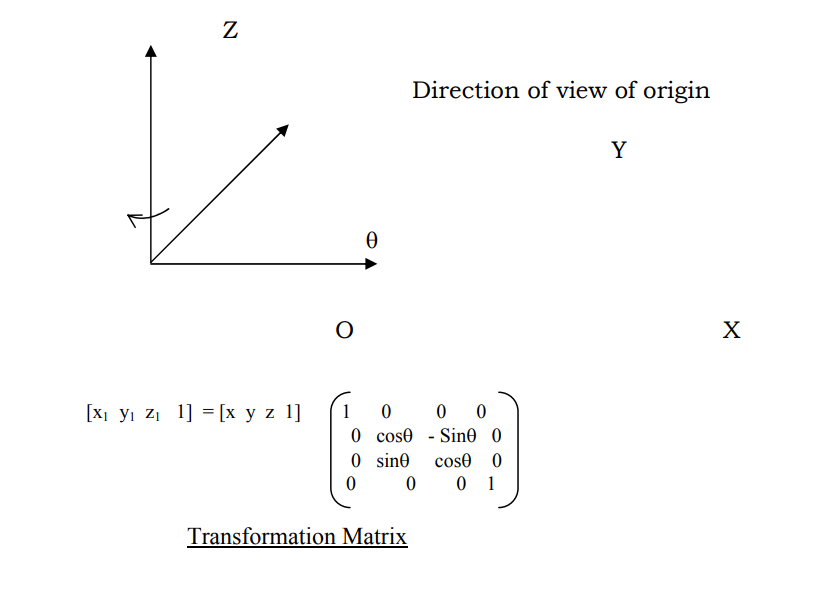
Now the other cases of rotation can be taken to be concatenations of the various operations
For example to rotate a point about an axis that passes through the origin, but does not coincide with any of the axes, as in the following figure
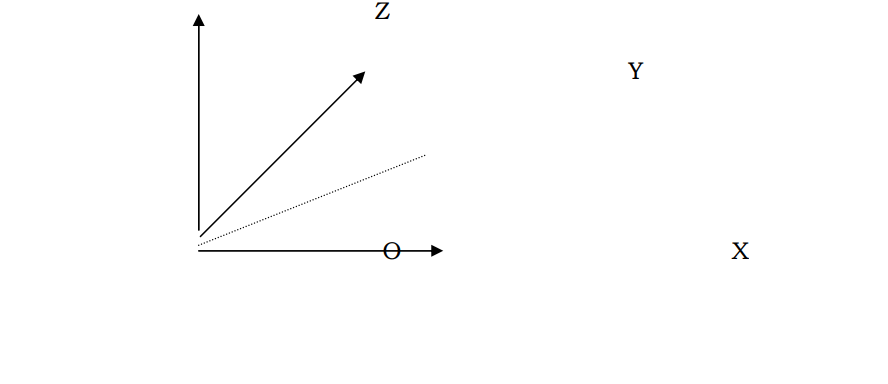
Suppose the axis passes through the origin, but does not coincide with any of the axes, then the axis itself is to be first aligned to one of the axes before doing the transformations. The sequence of events appears as follows.
- Rotate the axis through the desired angle to make it coincide with one of the axes. (Depending on with respect to which axis, it’s angle of deviation is available)
- Rotate the point (desired to be rotated) about this axis.
- Rotate the axis back to its original angle of deviation. In cases where the axis is an arbitrary axis passing through some points, but not the origin, the sequence lengthens
- Shift the point through which the axis points to the origin.
- Rotate the axis through an angle necessary to coincide it with one of the primary axes
- Rotate the point to be rotated about this axis.
- Rotate the axis back to it’s original inclination
- Shift the point from the origin to it’s original point.
