The performance of a scan conversion algorithm can be substantially improved by taking advantage of the property of coherence i.e. Given a pixel that is inside a polygon, it’s immediately adjacent pixels are most likely to be also inside the polygon. Similarity if a pixel is outside a polygon, most of its adjacent ones also will be most probably outside it. A corollary is that the coherence property changes only at the boundaries i.e. we will have to check the status of the pixels only at the boundaries and immediately adjacent to it, to find out whether the pixel lies inside or outside. The property of coherence can be applied to all its neighboring pixels and hence their status need not be checked individually. Consider the following example. Given a polygon, it is to be scan converted.
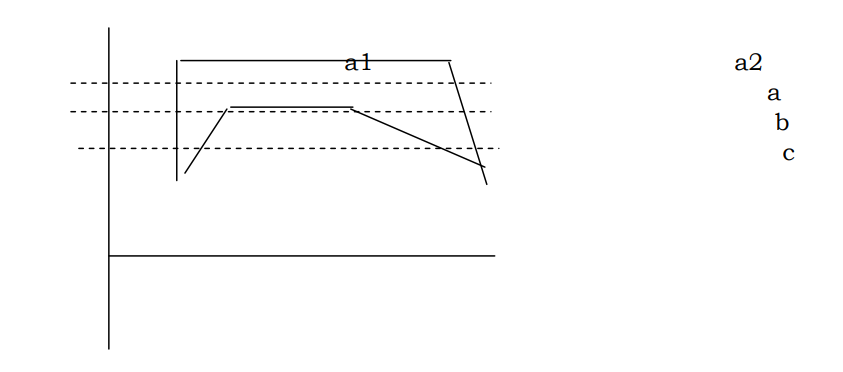
Suppose we want to identify all those pixels that lie inside the polygon and those that lie outside. This can be done in stages, scan line by scan line. Consider the scan line a. This is made up of a number of pixels. Beginning with left most point of the scan line, compute the intersections of the edges of the polygon with the particular scan line.
In this case these are two intersections (91 & a2). Starting at the left most pixels, all pixels lie outside the polygon up to the first intersection. From then on all pixels lie inside the polygon until the next intersection. Then afterwards, all pixels lie outside. Now consider a line b. It has more than two intersections with the polygon. In this case, the first intersection indicates the beginning of the series of pixels inside the polygon, the next intersection indicates that the following pixels will be inside the polygon and fourth intersection concludes the series.
