While mathematical formulae exist to compute the intersection of two straight lines (in this case, the edge under consideration and the straight line to be clipped) it comes computationally intensive and hence another efficient method has been developed. As you know, multiplication and division are most time consuming and hence an algorithm that minimizes on multiplications and divisions is always considered superior. The algorithm in question can be seen to be very efficient in minimizing the divisions that occur, when the intersection of two straight line are computed directly.
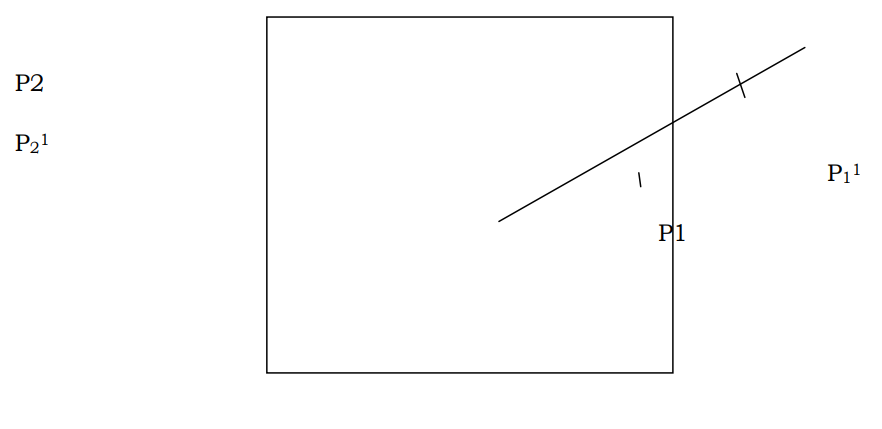
Consider a straight line P1 P2. point P11 is visible while the point P2 is not. The point is that we should find a point P1 which is the point farthest from P1 and still visible. Any point beyond P11 becomes invisible. The question is to find P11.
The algorithm processes by dividing the line P1 P2 at the middle, hence the name mid-point division. Let us say the point is P1 1 . This point, in this ease is visible. That means the farthest visible point away from P1 1 . So divide the segment P1 1 p2 at the middle. In this case, the new mid point P2 1 is invisible. So the farthest visible point is between P1 1 P2 1 . So divide the segment into two and so on, until you end up at a point that cannot be further divided. The segment P1 to this point is to be visible on the screen
