The basis of the Sutherland Hodgeman algorithms is that it is relatively easy to clip a polygon against one single edge of the screen at a time i.e. given a complete polygon, clip the entire polygon against one edge and take the resultant polygon to clip against a second edge and so on until all the four edges are covered. At first sight, it looks like a rather simplistic and too obvious a solution, but when put in practice this has been found to be extremely efficient
An algorithm can be represented by a set of vertices v1, v2, v3 ——- ——- vn which means there is an edge from v1 to v2, v2 to v3 . . . .. . . . vn to v1 (we consider only closed polygons and even after clipping would like to have closed polygons, the only difference being that the edges of the screen make for some of the edges of the newly formed, clipped polygon)
The algorithm tests each vertex vi (i=1,2 . . . . . . . .. . . . .n) in succession against a clipping edge e. Now e is an edge of the screen and has two sides. Any vertex lying on one side of the edge will be visible (which we call the visible side). While any other vertex will not be visible if it is on the other side (the invisible side). (For example for the top edge of the screen, any vertex above it is on the invisible side whereas any vertex below it is visible. Similarly for the left edge, any point to it’s left is invisible but an edge on it’s right is visible and so on).
Now coming back to the algorithm. It tests each vertex of the given polygon in turn against a clipping edge e. Vertices that lie on the visible side of e are included in the output polygon, while those that are on the invisible side are discarded. The next stage is to check whether the vertex vi (say) lies on the same side of e as it’s predecessor vi-1. If it does not, it’s intersection with the clipping edge e is to be evaluated and added to the output polygon.
Algorithm Sutherland – Hodgeman (v1, v2 v3 . . . .. . . . vn)
For i 1 to n do
if (i>1) then begin check whether the line
v[i] V[i-1] intersects the edge e, ifso, compute the intersection
and output the intersection point as the next out put vertex
end;
check always whether vi is on the visible
side of e
if so output vi
if i<n, go to (1)
else
Check whether the line Vn-V1 intersects e
if so, compute the intersection
and output it as the next edge
of the output polygon,
always return
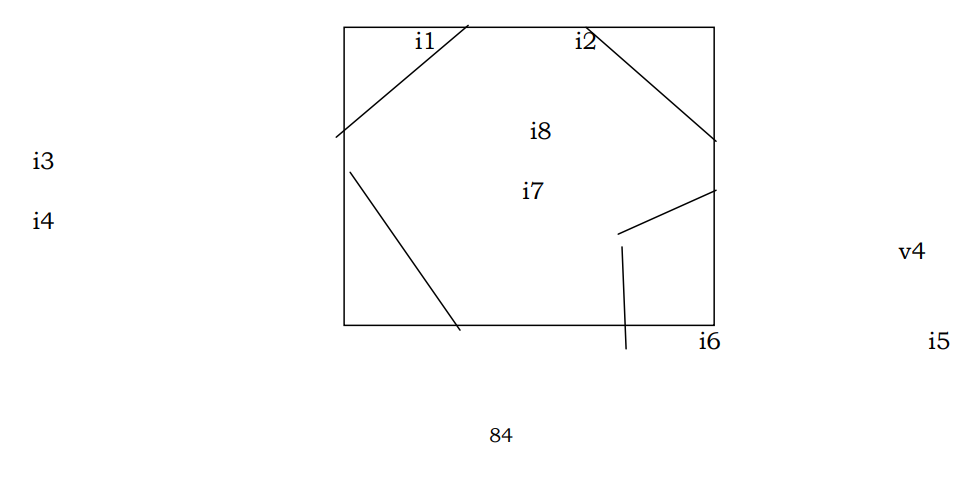
Now to illustrate this algorithm consider the 5 edges polygon below.
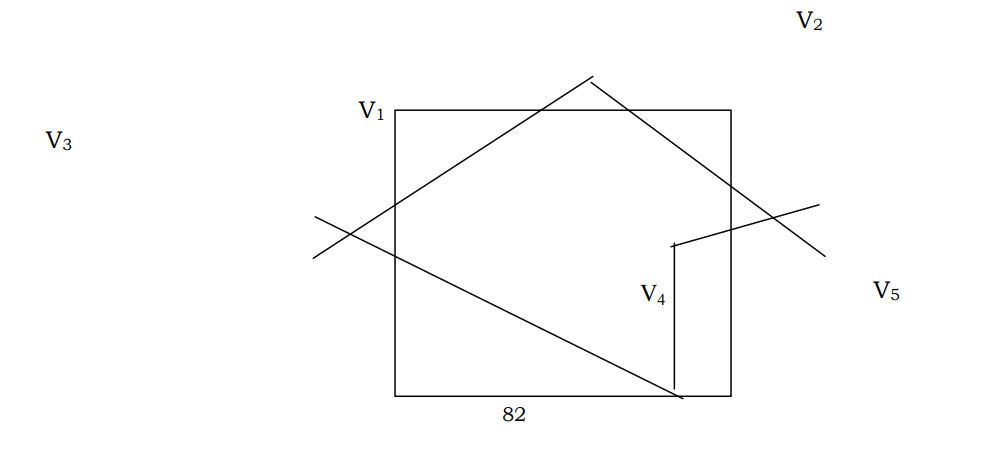
Now, let us consider ab as the clipping edge e. Beginning with v1 the vertex v1 is an the visible edge of ab so retain it in the output polygon now take the second vertex v2, the vertices v1, v2 are on different side of a. Compute the intersection of V1, V2 let it be i1, add i1 to the output polygon
Now consider the vertex v3, v2 and v3 are an different sides of ab. Compute the intersection of v2 and v3 with ab. Let it be i3. include i3 in the output polygon. Now consider v3, v4 and v5 are all on the same side (visible side) of the polygon, and hence when considered are after the other, they are included in the output polygon straightaway
Now the output polygon of stage (1) looks like in the figure below
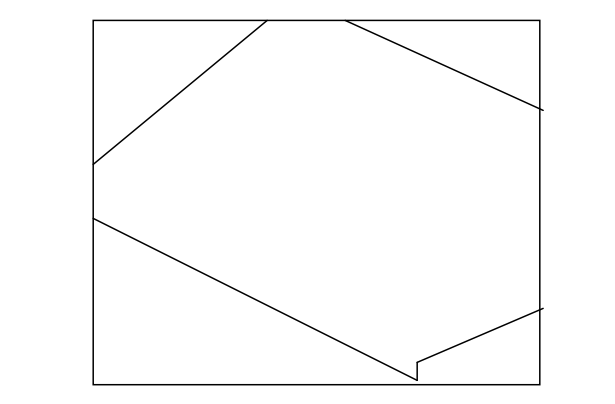
After going through two more clippings against the edges cd and da, the clipped figure looks like the one below