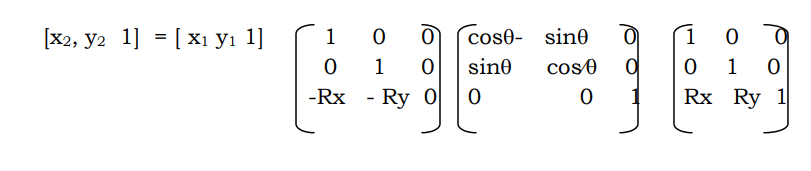
Often we do want to rotate our pictures about points other than the origin, like say the center of the picture we are talking of, or one of it’s vertices or may be a point on a neighboring picture. In this concluding section on transformations, we perform the operation of rotating a point (x1, y1) about another arbitrary point (Rx, Ry)
This is also supposed to provide you an insight about the ease with which matrix representation of operations allows us to Performa a sequence of operations.
First, how do we sequence the operations in the case?
Since we know how
i) to translate any point to any other point
ii) to rotate it by any angle w.r.t. the origin and
iii) to scale a point, we should be able to combine these
operations to do the required transformation.
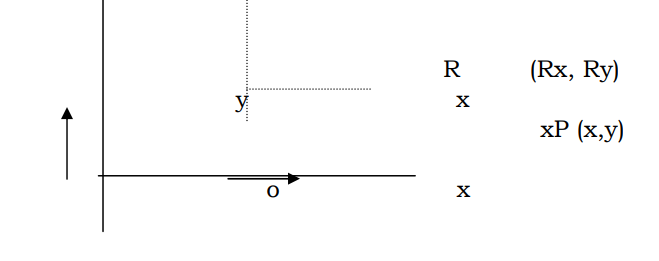
Now if we look at the figure, we know how to rotate the point w.r.t. O, the origin, whose coordinates are (0,0). But we should rotate it about the point R(Rs, Ry). Looking other way, we could have rotated P about R, if the coordinates of R were (0,0), or if we make the coordinates of R as (0,0). We can make the coordinates of R as (0,0) if we shift the rigin to R, (as shown by dotted lines).
If we do that, then we can rotate P about R. But we can shift the origin to R (or shift R to the origin, say) and make corresponding adjustments in the coordinates of P. (In practice, we simply evaluate what would be the value of (x1, y1), if instead o, R were the origin and we start measuring from R. This could be easily done by subtracting the difference of x and y values of R and origin (i.e. Rx & Ry) from the coordinates of (x, y). The new values, x1 1 and y1 1 referee to the coordinates w.r.t. R. Now since R is the origin, we know the formula for rotation P w.r.t. R by an angle. We do the operation and get the picture.
But the only hitch is that the whole sequence is about the point R, but it should have been w.r.t. origin. So, to get the desired picture from this, shift the origin back to O. Then we get the desired picture.
Now we can list the sequence of operations as follows.
i) Shift the origin to (Rx, Ry) from (0,0)
Using the matrix
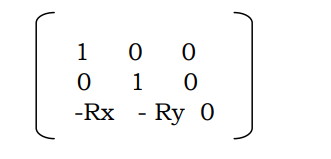
Rotate the point P(x1, y1) w.r.t. the (new) origin by
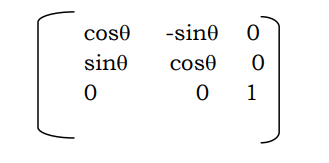
Shift the origin back to (0,0) by
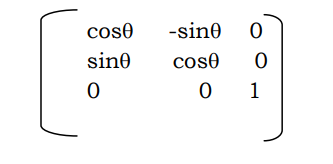
Hence the required point is