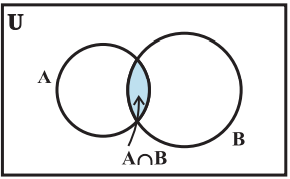
The intersection of two sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write
A ∩ B = {x : x ∈ A and x ∈ B}
venn diagram of intersection
Some Properties of Operation of Intersection
- A ∩ B = B ∩ A (Commutative law)
- ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) (Associative law)
- φ ∩ A = φ, U ∩ A = A (Law of φ and U)
- A ∩ A = A (Idempotent law)
- A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) (Distributive law )
Example of intersection
Example Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = { 2, 3, 5, 7 }. Find A ∩ B and
hence show that A ∩ B = B
Solution We have A ∩ B = { 2, 3, 5, 7 } = B. We
note that B ⊂ A and that A ∩ B = B
