Let U be the universal set and A a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A. Symbolically, we write A′ to denote the complement of A with respect to U. Thus
A′ = {x : x ∈ U and x ∉ A }. Obviously A′ = U – A
Example Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3, 5, 7, 9}. Find A′
Solution We note that 2, 4, 6, 8, 10 are the only elements of U which do not belong to
A. Hence A′ = { 2, 4, 6, 8,10 }
Venn diagram of Complement of a Set
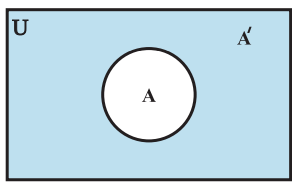
Some Properties of Complement Sets
- Complement laws: (i) A ∪ A′ = U (ii) A ∩ A′ = φ
- De Morgan’s law: (i) (A ∪ B)´ = A′ ∩ B′ (ii) (A ∩ B)′ = A′ ∪ B′
- Law of double complementation : (A′)′ = A
- Laws of empty set and universal set φ′ = U and U′ = φ
