The tower of Hanoi is one of the main applications of recursion. It says, ‘if you can solve n–1 cases, then you can easily solve the nth case’
The following code implements the solution of the tower of Hanoi problem
#include <stdio.h>
int main()
{
int n;
printf("\n Enter the number of rings: ");
scanf("%d", &n);
move(n,'A', 'C', 'B');
return 0;
}
void move(int n, char source, char dest, char spare)
{
if (n==1)
printf("\n Move from %c to %c",source,dest);
else
{
move(n–1,source,spare,dest);
move(1,source,dest,spare);
move(n–1,spare,dest,source);
}
}
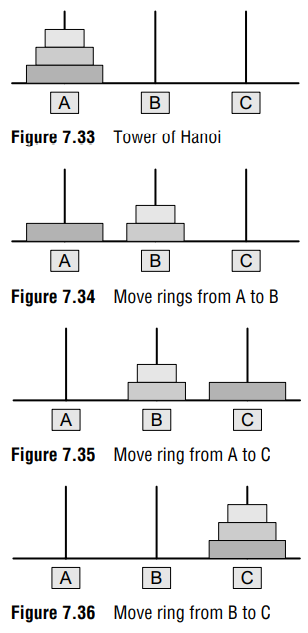
To summarize, the solution to our problem of moving n rings from A to C using B as spare can be given as:
Base case: if n=1
- Move the ring from A to C using B as spare
Recursive case:
- Move n – 1 rings from A to B using C as spare
- Move the one ring left on A to C using B as spare
- Move n – 1 rings from B to C using A as spare
The advantages of using a recursive program include the following:
- Recursive solutions often tend to be shorter and simpler than non-recursive ones.
- Code is clearer and easier to use
- Recursion works similar to the original formula to solve a problem.
- Recursion follows a divide and conquer technique to solve problems
- In some (limited) instances, recursion may be more efficient
The drawbacks/disadvantages of using a recursive program include the following:
- For some programmers and readers, recursion is a difficult concept.
- Recursion is implemented using system stack. If the stack space on the system is limited, recursion to a deeper level will be difficult to implement.
- Aborting a recursive program in midstream can be a very slow process.
- Using a recursive function takes more memory and time to execute as compared to its non recursive counterpart
- It is difficult to find bugs, particularly while using global variables
