Sparse matrix is a matrix that has large number of elements with a zero value. In order to efficiently utilize the memory, specialized algorithms and data structures that take advantage of the sparse structure should be used. If we apply the operations using standard matrix structures and algorithms to sparse matrices, then the execution will slow down and the matrix will consume large amount of memory. Sparse data can be easily compressed, which in turn can significantly reduce memory usage.
There are two types of sparse matrices. In the first type of sparse matrix, all elements above the main diagonal have a zero value. This type of sparse matrix is also called a (lower) triangonal matrix because if you see it pictorially, all the elements with a non-zero value appear below the diagonal. In a lower triangular matrix, Ai,j=0 where i<j. An n×n lower-triangular matrix A has one non-zero element in the first row, two non-zero elements in the second row and likewise n non-zero elements in the nth row

matrix
To store a lower-triangular matrix efficiently in the memory, we can use a one-dimensional array which stores only non-zero elements. The mapping between a two-dimensional matrix and a one-dimensional array can be done in any one of the following ways:
Row-wise mapping—Here the contents of array A[] will be {1, 5, 3, 2, 7, –1, 3, 1, 4, 2, –9, 2, –8, 1, 7}
Column-wise mapping—Here the contents of array A[] will be {1, 5, 2, 3, –9, 3, 7, 1, 2, –1, 4, –8, 2, 1, 7}
In an upper-triangular matrix, Ai,j=0 where i>j. An n×n upper-triangular matrix A has n non-zero elements in the first row, n–1 non-zero elements in the second row and likewise one non-zero element in the nth row

matrix
There is another variant of a sparse matrix, in which elements with a non-zero value can appear only on the diagonal or immediately above or below the diagonal. This type of matrix is also called a tri-diagonal matrix. Hence in a tridiagonal matrix, Ai,j=0, where |i – j| > 1. In a tridiagonal matrix, if elements are present on
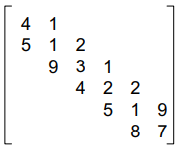
matrix
- the main diagonal, it contains non-zero elements for i=j. In all, there will be n elements.
- below the main diagonal, it contains non-zero elements for i=j+1. In all, there will be n–1 elements.
- above the main diagonal, it contains non-zero elements for i=j–1. In all, there will be n–1 elements
