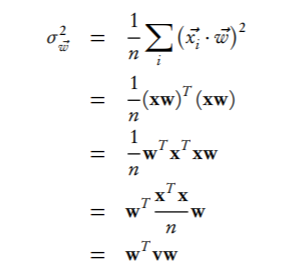Principal components analysis (PCA) is one of a family of techniques for taking high-dimensional data, and using the dependencies between the variables to represent it in a more tractable, lower-dimensional form, without losing too much information.
PCA is one of the simplest and most robust ways of doing such dimensionality reduction. It is also one of the oldest, and has been rediscovered many times in many fields, so it is also known as the Karhunen-Loève transformation, the Hotelling transformation, the method of empirical orthogonal functions, and singular value decomposition
Mathematics of Principal Components
There are several equivalent ways of deriving the principal components mathematically. The simplest one is by finding the projections which maximize the variance. The first principal component is the direction in space along which projections have the largest variance. The second principal component is the direction which maximizes variance among all directions orthogonal to the first. The kth component is the variance-maximizing direction orthogonal to the previous k − 1 components. There are p principal components in all
Maximizing Variance
Accordingly, let’s maximize the variance! Writing out all the summations grows tedious, so let’s do our algebra in matrix form. If we stack our n data vectors into an n × p matrix, x, then the projections are given by xw, which is an n ×1 matrix. The variance is