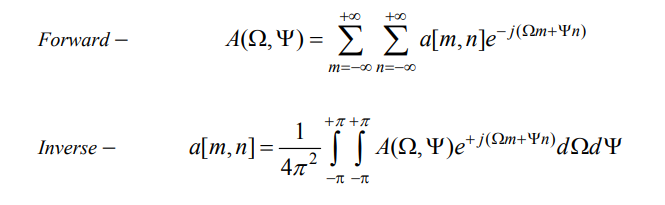The Fourier transform produces another representation of a signal, specifically a representation as a weighted sum of complex exponentials. Because of Euler’s formula
ejq =cos(q) + jsin(q)
where j2 = −1, we can say that the Fourier transform produces a representation of a (2D) signal as a weighted sum of sines and cosines. The defining formulas for the forward Fourier and the inverse Fourier transforms are as follows. Given an image a and its Fourier transform A, then the forward transform goes from the spatial domain (either continuous or discrete) to the frequency domain which is always continuous
The specific formulas for transforming back and forth between the spatial domain and the frequency domain are given below
In 2D continuous space:

In 2D discrete space: