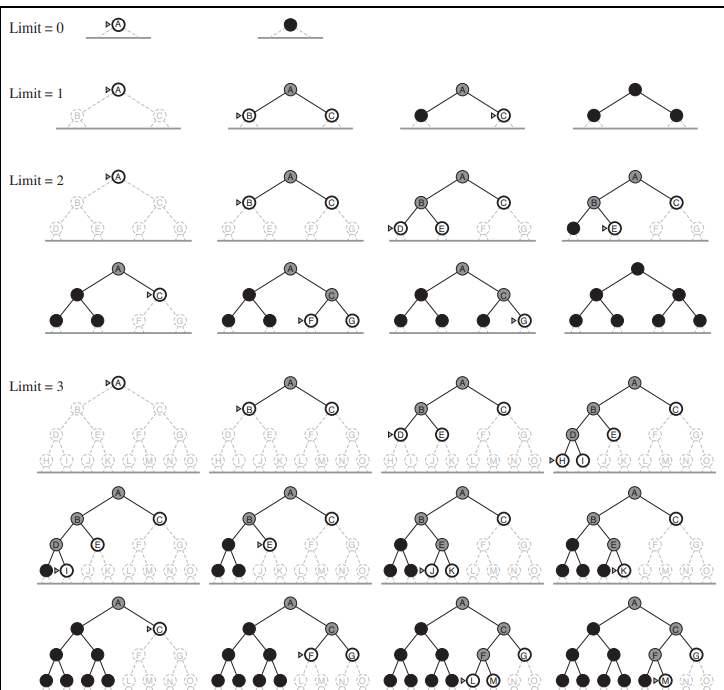
Iterative deepening search (or iterative deepening depth-first search) is a general strategy, often used in combination with depth-first tree search, that finds the best depth limit. It does this by gradually increasing the limit—first 0, then 1, then 2, and so on—until a goal is found. This will occur when the depth limit reaches d, the depth of the shallowest goal node.
Like depth-first search, its memory requirements are modest: O(bd) to be precise. Like breadth-first search, it is complete when the branching factor is finite and optimal when the path cost is a nondecreasing function of the depth of the node. Figure shows four iterations of ITERATIVE-DEEPENING-SEARCH on a binary search tree, where the solution is found on the fourth iteration
function ITERATIVE-DEEPENING-SEARCH(problem) returns a solution, or failure
for depth = 0 to ∞ do
result ← DEPTH-LIMITED-SEARCH(problem, depth)
if result |= cutoff then return result
Total number of nodes generated in the worst case is
N(IDS)=(d)b + (d − 1)b2 + ··· + (1)bd
which gives a time complexity of O(bd)—asymptotically the same as breadth-first search. There is some extra cost for generating the upper levels multiple times, but it is not large
For example, if b = 10 and d = 5, the numbers are
N(IDS) = 50 + 400 + 3, 000 + 20, 000 + 100, 000 = 123, 450
N(BFS) = 10 + 100 + 1, 000 + 10, 000 + 100, 000 = 111, 110
In general, iterative deepening is the preferred uninformed search method when the search space is large and the depth of the solution is not known
