A Shannon-Fano tree is built according to a specification designed to define an effective code table. The actual algorithm is simple:
- For a given list of symbols, develop a corresponding list of probabilities or frequency counts so that each symbol’s relative frequency of occurrence is known
- Sort the lists of symbols according to frequency, with the most frequently occuring symbols at the top and the least common at the bottom.
- Divide the list into two parts, with the total frequency counts of the upper half being as close to the total of the bottom half as possible.
- The upper half of the list is assigned the binary digit 0, and the lower half is assigned the digit 1. This means that the codes for the symbols in the first half will all start with 0, and the codes in the second half will all start with 1
- Recursively apply the steps 3 and 4 to each of the two halves, subdividing groups and adding bits to the codes until each symbol has become a corresponding code leaf on the tree.
Table of symbol frequencies
| Symbol | Count |
|---|---|
| A | 15 |
| B | 7 |
| C | 6 |
| D | 6 |
| E | 5 |
Putting the dividing line between symbols B and C assigns a count of 22 to the upper group and 17 to the lower, the closest to exactly half. This means that A and B will each have a code that starts with a 0 bit, and C, D, and E are all going to start with a 1 as shown:
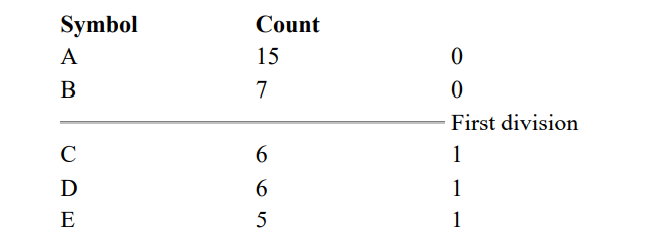
Subsequently, the upper half of the table gets a new division between A and B, which puts A on a leaf with code 00 and B on a leaf with code 01. After four division procedures, a table of codes results. In the final table, the three symbols with the highest frequencies have all been assigned 2-bit codes, and two symbols with lower counts have 3-bit codes as shown next
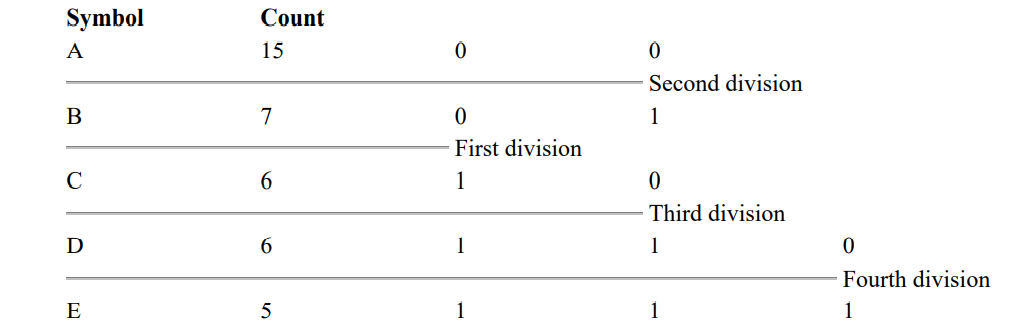
That symbols with the higher probability of occurence have fewer bits in their codes indicates we are on the right track. The formula for information content for a given symbol is the negative of the base two logarithm of the symbol’s probability. For our theoretical message, the information content of each symbol, along with the total number of bits for that symbol in the message, are found in the following table.
| Symbol | Count | Info Cont | Info Bits |
|---|---|---|---|
| A | 15 | 1.38 | 20.68 |
| B | 7 | 2.48 | 17.35 |
| C | 6 | 2.70 | 16.20 |
| D | 6 | 2.70 | 16.20 |
| E | 5 | 2.96 | 14.82 |
The information for this message adds up to about 85.25 bits. If we code the characters using 8-bit ASCII characters, we would use 39 × 8 bits, or 312 bits. Obviously there is room for improvement.
When we encode the same data using Shannon-Fano codes, we come up with some pretty good numbers, as shown below
| Symbol | Count | Info Cont. | Info Bits | SF Size | SF Bits |
|---|---|---|---|---|---|
| A | 15 | 1.38 | 20.68 | 2 | 30 |
| B | 7 | 2.48 | 17.35 | 2 | 14 |
| C | 6 | 2.70 | 16.20 | 2 | 12 |
| D | 6 | 2.70 | 16.20 | 3 | 18 |
| E | 5 | 2.96 | 14.82 | 3 | 15 |
With the Shannon-Fano coding system, it takes only 89 bits to encode 85.25 bits of information. Clearly we have come a long way in our quest for efficient coding methods. And while Shannon-Fano coding was a great leap forward, it had the unfortunate luck to be quickly superseded by an even more efficient coding system: Huffman coding.
